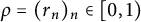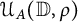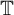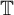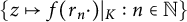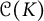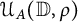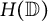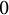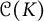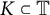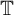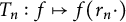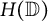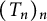Given a sequence 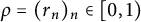$\varrho =(r_n)_n\in [0,1)$ tending to 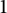$1$, we consider the set 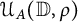${\mathcal {U}}_A({\mathbb {D}},\varrho )$ of Abel universal functions consisting of holomorphic functions f in the open unit disk 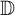$\mathbb {D}$ such that for any compact set K included in the unit circle 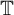${\mathbb {T}}$, different from 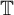${\mathbb {T}}$, the set 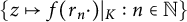$\{z\mapsto f(r_n \cdot )\vert _K:n\in \mathbb {N}\}$ is dense in the space 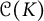${\mathcal {C}}(K)$ of continuous functions on K. It is known that the set 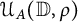${\mathcal {U}}_A({\mathbb {D}},\varrho )$ is residual in 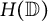$H(\mathbb {D})$. We prove that it does not coincide with any other classical sets of universal holomorphic functions. In particular, it is not even comparable in terms of inclusion to the set of holomorphic functions whose Taylor polynomials at 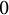$0$ are dense in 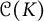${\mathcal {C}}(K)$ for any compact set 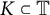$K\subset {\mathbb {T}}$ different from 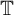${\mathbb {T}}$. Moreover, we prove that the class of Abel universal functions is not invariant under the action of the differentiation operator. Finally, an Abel universal function can be viewed as a universal vector of the sequence of dilation operators 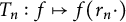$T_n:f\mapsto f(r_n \cdot )$ acting on 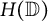$H(\mathbb {D})$. Thus, we study the dynamical properties of 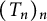$(T_n)_n$ such as the multiuniversality and the (common) frequent universality. All the proofs are constructive.

Differential changes of time involving two parameters are considered. Universal expressions for dynamical variables of interest in Keplerian motion allow us to reduce the integration of the time transformations to that of integrands depending on an eccentric-like universal anomaly. Elliptic integrals and functions are required to complete the integration.