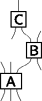
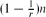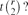Refine search
Actions for selected content:
48276 results in Computer Science
Preface to special issue: Developments In Computational Models 2010
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 201-203
-
- Article
-
- You have access
- Export citation
Constraining rule-based dynamics with types
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 272-289
-
- Article
- Export citation
Equilibrium and termination II: the case of Petri nets
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 290-307
-
- Article
- Export citation
Towards a Weighted Version of the Hajnal–Szemerédi Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 346-350
-
- Article
- Export citation
Multi-level modelling via stochastic multi-level multiset rewriting†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 471-503
-
- Article
- Export citation
Extended phase map decompositions for unitaries
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 360-385
-
- Article
- Export citation
A formalism-local framework for general probabilistic theories, including quantum theory
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 399-440
-
- Article
- Export citation
MSC volume 23 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Two-domain DNA strand displacement
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 247-271
-
- Article
- Export citation
Comparing the globalness of bipartite unitary operations: delocalisation power, entanglement cost and entangling power†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 454-470
-
- Article
- Export citation
Open-graphs and monoidal theories†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 23 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 308-359
-
- Article
- Export citation
Retrieving implicit positive meaning from negated statements
-
- Journal:
- Natural Language Engineering / Volume 20 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 26 February 2013, pp. 501-535
-
- Article
- Export citation
NLE volume 19 issue 2 Cover and Front matter
-
- Journal:
- Natural Language Engineering / Volume 19 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 22 February 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Preface to special issue on Knowledge Engineering for Planning and Scheduling
-
- Journal:
- The Knowledge Engineering Review / Volume 28 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2013, pp. 117-119
-
- Article
-
- You have access
- HTML
- Export citation
NLE volume 19 issue 2 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 19 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 22 February 2013, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Acquiring planning domain models using LOCM
-
- Journal:
- The Knowledge Engineering Review / Volume 28 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2013, pp. 195-213
-
- Article
- Export citation
The Size of the Largest Part of Random Weighted Partitions of Large Integers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 21 February 2013, pp. 433-454
-
- Article
- Export citation