Refine search
Actions for selected content:
48585 results in Computer Science
MSC volume 1 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Structures in Computer Science / Volume 1 / Issue 2 / July 1991
- Published online by Cambridge University Press:
- 04 March 2009, p. b1
-
- Article
-
- You have access
- Export citation
Temporal Structures
-
- Journal:
- Mathematical Structures in Computer Science / Volume 1 / Issue 2 / July 1991
- Published online by Cambridge University Press:
- 04 March 2009, pp. 179-213
-
- Article
- Export citation
Author Index to Volume 1
-
- Journal:
- Mathematical Structures in Computer Science / Volume 1 / Issue 3 / November 1991
- Published online by Cambridge University Press:
- 04 March 2009, p. 405
-
- Article
- Export citation
Engeler's scientific work
-
- Journal:
- Mathematical Structures in Computer Science / Volume 2 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 04 March 2009, pp. 111-117
-
- Article
- Export citation
Dynamic labeled 2-structures
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. 433-455
-
- Article
- Export citation
Simulating expansions without expansions
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. 315-362
-
- Article
- Export citation
Equivalence and difference between institutions: simulating Horn Clause Logic with based algebras
-
- Journal:
- Mathematical Structures in Computer Science / Volume 5 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 04 March 2009, pp. 189-215
-
- Article
- Export citation
An imperative language based on distributive categories
-
- Journal:
- Mathematical Structures in Computer Science / Volume 2 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 04 March 2009, pp. 249-256
-
- Article
- Export citation
Categorical models for non-extensional λ-calculi and combinatory logic
-
- Journal:
- Mathematical Structures in Computer Science / Volume 2 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 04 March 2009, pp. 327-357
-
- Article
- Export citation
MSC volume 4 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Sheaf semantics for concurrent interacting objects
-
- Journal:
- Mathematical Structures in Computer Science / Volume 2 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 04 March 2009, pp. 159-191
-
- Article
- Export citation
Church-Rooser property and homology of monoids
-
- Journal:
- Mathematical Structures in Computer Science / Volume 1 / Issue 3 / November 1991
- Published online by Cambridge University Press:
- 04 March 2009, pp. 297-326
-
- Article
- Export citation
Equational axioms for regular sets
-
- Journal:
- Mathematical Structures in Computer Science / Volume 3 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 04 March 2009, pp. 1-24
-
- Article
- Export citation
Causal dependencies in multiplicative linear logic with MIX
-
- Journal:
- Mathematical Structures in Computer Science / Volume 5 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 04 March 2009, pp. 351-380
-
- Article
- Export citation
Author Index to Volume 4
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 04 March 2009, p. 513
-
- Article
- Export citation
A category-theoretic account of program modules
-
- Journal:
- Mathematical Structures in Computer Science / Volume 1 / Issue 1 / March 1991
- Published online by Cambridge University Press:
- 04 March 2009, pp. 103-139
-
- Article
- Export citation
A universality theorem for PCF with recursive types, parallel-or and ∃
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. 111-115
-
- Article
- Export citation
Categories, relations and dynamic programming
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. 33-69
-
- Article
- Export citation
Connected limits, familial representability and Artin glueing
-
- Journal:
- Mathematical Structures in Computer Science / Volume 5 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 04 March 2009, pp. 441-459
-
- Article
- Export citation
MSC volume 4 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Structures in Computer Science / Volume 4 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 04 March 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
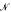 →
→ 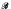 , where
, where 