A notion of bilattice was first proposed by Ginsberg as a general framework for many applications. Related notions were further investigated and applied for various goals by Fitting. In the present paper a general definition of bilattices is proposed, which covers all particular cases that have actually been used in the literature. It is shown also that in the finite case every bilattice in our sense is graphically representable by a special type of a two-dimensional diagram.

This paper tackles the problem of constructing a compact, point-free proof of the associativity of demonic composition of binary relations and its distributivity through demonic choice. In order to achieve this goal, a definition of demonic composition is proposed in which angelic composition is restricted by means of a so-called ‘monotype factor’. Monotype factors are characterised by a Galois connection similar to the Galois connection between composition and factorisation of binary relations. The identification of such a connection is argued to be highly conducive to the desired compactness of calculation.

In this paper we study partial equivalence relations (PERs) over graph models of the λcalculus. We define categories of PERs that behave like predomains, and like domains. These categories are small and complete; so we can solve domain equations and construct polymorphic types inside them. Upper, lower and convex powerdomain constructions are also available, as well as interpretations of subtyping and bounded quantification. Rather than performing explicit calculations with PERs, we work inside the appropriate realizability topos: this is a model of constructive set theory in which PERs, can be regarded simply as special kinds of sets. In this framework, most of the definitions and proofs become quite smple and attractives. They illustrative some general technicques in ‘synthetic domain theory’ that rely heavily on category theory; using these methods, we can obtain quite powerful results about classes of PERs, even when we know very little about their internal structure.

This paper exhibits accurate encodings of the λ-calculus in the π-calculus. The former is canonical for calculation with functions, while the latter is a recent step (Milner et al. 1989) towards a canonical treatment of concurrent processes. With quite simple encodings, two λ-calculus reduction strategies are simulated very closely; each reduction in λ-calculus is mimicked by a short sequence of reductions in π-calculus. Abramsky's precongruence of applicative bisimulation (Abramsky 1989) over λ-calculus is compared with that induced by the encoding of the lazy λ-calculus into π-calculus; a similar comparison is made for call-by-value λ-calculus.

Distributive category theory is the study of categories with two monoidal structures, one of which “distributes” over the other in some manner. When these are the product and coproduct, this distribution is taken to be the law

which asserts that the obvious canonical map has an inverse. A distributive category is here taken to mean a category with finite products and binary coproducts such that this law is satisfied.

In any distributive category the coproduct of the final object with itself, 1 + 1, forms a boolean algebra. Thus, maps into 1 + 1 provide a boolean logic: if each such map recognizes a unique subobject, the category is a recognizable distributive category. If, furthermore, the category is such that these recognizers classify detachable subobjects (coproduct embeddings), it is an extensive distributive category.

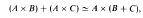
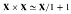Extensive distributive categories can be approached in various ways. For example, recognizable distributive categories, in which coproducts are disjoint or all preinitials are isomorphic, are extensive. Also, a category X having finite products and binary coproducts satisfying the slice equation (due to Schanuel and Lawvere) is extensive. This paper describes a series of embedding theorems. Any distributive category has a full faithful embedding into a recognizable distributive category. Any recognizable distributive category can be "solidified" faithfully to produce an extensive distributive category. Any extensive distributive category can be embedded into a topos.

A peculiar source of extensive distributive categories is the coproduct completion of categories with familial finite products. In particular, this includes the coproduct completion of cartesian categories, which is serendipitously, therefore, also the distributive completion. Familial distributive categories can be characterized as distributive categories for which every object has a finite decomposition into indecomposables.

We introduce a new class of higher order rewriting systems, called Interaction Systems (IS's). IS's are derived from Lafont's (Intuitionistic) Interaction Nets (Lafont 1990) by dropping the linearity constraint. In particular, we borrow from Interaction Nets the syntactical bipartitions of operators into constructors and destructors and the principle of binary interaction. As a consequence, IS's are a subclass of Klop's Combinatory Reduction Systems (Klop 1980), where the Curry-Howard analogy still ‘makes sense’. Destructors and constructors, respectively, correspond to left and right logical introduction rules: interaction is cut and reduction is cut-elimination.

Interaction Systems have been primarily motivated by the necessity of extending the practice of optimal evaluators for λ-calculus (Lamping 1990; Gonthier et al. 1992a) to other computational constructs such as conditionals and recursion. In this paper we focus on the theoretical aspects of optimal reductions. In particular, we generalize the family relation in Lévy (1978; 1980), thus defining the amount of sharing an optimal evaluator is required to perform. We reinforce our notion of family by approaching it in two different ways (generalizing labelling and extraction in Levy (1980)) and proving their coincidence. The reader is referred to Asperti and Laneve (1993c) for the paradigmatic description of optimal evaluators of IS's.

Argumentation is a proof theoretic paradigm for reasoning under uncertainty. Whereas a ‘proof’ establishes its conclusion outright, an ‘argument’ can only lend a measure of support. Thus, the process of argumentation consists of identifying all the arguments for a particular hypothesis φ, and then calculating the support for φ from the weight attached to these individual arguments. Argumentation has been incorporated as the inference mechanism of a large scale medical expert system, the ‘Oxford System of Medicine’ (OSM), and it is therefore important to demonstrate that the approach is theoretically justified. This paper provides a formal semantics for the notion of argument embodied in the OSM. We present a categorical account in which arguments are the arrows of a semilattice enriched category. The axioms of a cartesian closed category are modified to give the notion of an ‘evidential closed category’, and we show that this provides the correct enriched setting in which to model the connectives of conjunction (&) and implication (⇒).

Finally, we develop a theory of ‘confidence measures’ over such categories, and relate this to the Dempster-Shafer theory of evidence.

The notion of semi-functor was introduced in Hayashi (1985) in order to make possible a category-theoretical characterization of models of the non-extensional typed lambda calculus. Motivated by the further use of semi-functors in Martini (1987), Jacobs (1991) and Hoofman (1992a), (1992b) and (1992c), we consider the general theory of semi-functors in this paper. It turns out that the notion of semi natural transformation plays an important part in this theory, and that various categorical notions involving semi-functors can be viewed as 2-categorical notions in the 2-category of categories, semi-functors and semi natural transformations. In particular, we find that the notion of normal semi-adjunction as defined in Hayashi (1985) is the canonical generalization of the notion of adjunction to the world of semi-functors. Further topics covered in this paper are the relation between semi-functors and splittings, the Karoubi envelope construction, semi-comonads, and a semi-adjoint functor theorem.

We study a type system with a notion of subtyping that involves a largest type ⊤, a smallest type ⊥, atomic coercions between base types, and the usual ordering of function types. We prove that any λ-term typable in this system is strongly normalizing, which solves an open problem of Thatte. We also prove that the fragment without ⊥ types has strictly fewer terms. This demonstrates that ⊥ adds power to a type system.

We axiomatize permutation equivalence in term rewriting systems and Klop’s orthogonal Combinatory Reduction Systems (Klop 1980). The axioms for the former are provided by the general approach proposed by Meseguer (Meseguer 1992). The latter need extra axioms modelling the interplay between reductions and the operation of substitution.

As a consequence of this work, the definition of permutation equivalence is rid of residual calculi, which are heavy in general.

Inspired by the work of S. Kaplan on positive/negative conditional rewriting, we investigate initial semantics for algebraic specifications with Gentzen formulas. Since the standard initial approach is limited to conditional equations (i.e. positive Horn formulas), the notion of semi-initial and quasi-initial algebras is introduced, and it is shown that all specifications with (positive) Gentzen formulas admit quasi-initial models.

The whole approach is generalized to the parametric case where quasi-initiality generalizes to quasi-freeness. Since quasi-free objects need not be isomorphic, the persistency requirement is added to obtain a unique semantics for many interesting practical examples. Unique persistent quasi-free semantics can be described as a free construction if the homomorphisms of the parameter category are suitably restricted. Furthermore, it turns out that unique persistent quasi-free semantics applies especially to specifications where the Gentzen formulas can be interpreted as hierarchical positive/negative conditional equations. The data type constructor of finite function spaces is used as an example that does not admit a correct initial semantics, but does admit a correct unique persistent quasi-initial semantics. The example demonstrates that the concepts introduced in this paper might be of some importance in practical applications.

We present a new model of classical linear logic based on the notion of strong stability that was introduced recently in a work about sequentiality written jointly with Antonio Bucciarelli.

Bilattices were introduced and applied by Ginsberg and Fitting for a diversity of applications, such as truth maintenance systems, default inferences and logic programming. In this paper we investigate the structure and properties of a particularly important class of bilattices called interlaced bilattices, which were introduced by Fitting. The main results are that every interlaced bilattice is isomorphic to the Ginsberg-Fitting product of two bounded lattices and that the variety of interlaced bilattices is equivalent to the variety of bounded lattices with two distinguishable distributive elements, which are complements of each other. This implies that interlaced bilattices can be characterized using a finite set of equations. Our results generalize to interlaced bilattices some results of Ginsberg, Fitting and Jónsson for distributive bilattices.

We consider the problem of mechanically constructing abstract machines from operational semantics, producing intermediate-level specifications of evaluators guaranteed to be correct with respect to the operational semantics. We construct these machines by repeatedly applying correctness-preserving transformations to operational semantics until the resulting specifications have the form of abstract machines. Though not automatable in general, this approach to constructing machine implementations can be mechanized, providing machine-verified correctness proofs. As examples, we present the transformation of specifications for both call-by-name and call-by-value evaluation of the untyped λ-calculus into abstract machines that implement such evaluation strategies. We also present extensions to the call-by-value machine for a language containing constructs for recursion, conditionals, concrete data types, and built-in functions. In all cases, the correctness of the derived abstract machines follows from the (generally transparent) correctness of the initial operational semantic specification and the correctness of the transformations applied.

In the literature ther are two main notins of model for the second order λ-calculus: one by Bruce, Meyer and Mitchell (the BMM-model, for short) in set-theoretical formulation and one category-theoretical by Seely. Here we generalise Seely's notion, using semifunctors and semi-adjunctions from Hayashi, and introduce λ2-algebras, λη2-algebras, λ2-models and λη-models, similarly to the untyped λ-calculus. Non-extensional abstraction of both term and type variables is described by semi-adjunctions (essentially as in Martini's thesis). We show that also for second order sume, the β-(and commutation!) conversions correspond to semi-functoriality and that the (additional) η-conversion corresponds to ordinary fuctioriality.

In the above framework various examples – well known ones and variations – are described. Also, we determine the place of the BMM-models; an earlier version of the latter has been reported by Jacobs.