We propose a new framework for representing logics, called LF+, which is based on the Edinburgh Logical Framework. The new framework allows us to give, apparently for the first time, general definitions that capture how well a logic has been represented. These definitions are possible because we are able to distinguish in a generic way that part of the LF+ entailment corresponding to the underlying logic. This distinction does not seem to be possible with other frameworks. Using our definitions, we show that, for example, natural deduction first-order logic can be well-represented in LF+, whereas linear and relevant logics cannot. We also show that our syntactic definitions of representation have a simple formulation as indexed isomorphisms, which both confirms that our approach is a natural one and provides a link between type-theoretic and categorical approaches to frameworks.

In this paper we try to shed some light on the similarities and differences in the different approaches denning the notions of implementation and implementation correctness. For obvious reasons, we do not discuss all existing approaches individually. Instead, a formal framework is introduced in order to discuss the most important ones. Additionally, we discuss some issues, which in our opinion are often misunderstood, concerning transitivity of implementation correctness and its role in the software development process. In particular, on the one hand, we show that for reasonable notions of implementation, it is almost impossible to prove transitivity of implementation correctness at the specification level. On the other hand, we show that this is not really important if the programming language satisfies the properties of horizontal and vertical composition.

Two imperative programming language phrases interfere when one writes to a storage variable that the other reads from or writes to. Reynolds has described an elegant linguistic approach to controlling interference in which a refinement of typed λ-calculus is used to limit sharing of storage variables; in particular, different identifiers are required never to interfere. This paper examines semantic foundations of the approach.

We describe a category that has (an abstraction of) interference information built into all objects and maps. This information is used to define a ‘tensor’ product whose components are required never to interfere. Environments are defined using the tensor, and procedure types are obtained via a suitable adjunction. The category is a model of intuitionistic linear logic. Reynolds' concept of passive type - i.e. types for phrases that do not write to any storage variables - is shown to be closely related, in this model, to Girard's ‘of course’ modality.

There are two ways to present this work; the most efficient is of course to start with the main syntactical definitions, and to end with semantics: this is the presentation that we follow in the body of the text: section 1, syntex; section 2, semantics. Another possibility is to follow the order of discovery of the concepts, which (as expected) starts with the semantics and ends with the syntex; we adopt this second way for our introduction, hoping that this orthogonal look at the same object will help to apprehend the concepts.

High-level replacement systems are formulated in an axiomatic algebraic framework based on categories pushouts. This approach generalizes the well-known algebraic approach to graph grammars and several other types of replacement systems, especially the replacement of algebraic specifications which was recently introduced for a rule-based approach to modular system design.

in this paper basic notions like productions, derivations, parellel and sequential independence are introduced for high-level replacement syetms leading to Church-Rosser, Parallelism and concurrency Theorems previously shown in the literature for special cases only. In the general case of high-level replacement systems specific conditions, called HLR1- and HLR2-conditions, are formulated in order to obtain these results.

Several examples of high-level replacement systems are discussed and classified w.r.t. HLR1- and HLR2-conditions showing which of the results are valid in each case.

Categorical constructions inherent to a theory of algebras with strict partial operations are presented and exploited to provide a categorical deduction calculus for conditional existence equations and an alternative definition of such algebras based on the notion of syntactic categories. A compact presentation of the structural theory of parameterized (partial) specifications is given using the categorical approach. This theory is shown to be suitable for providing initial semantics as well as the compositionality results necessary for the definition of specification languages like ACT ONE and ACT TWO

In the theory of denotational semantics of programming languages, several authors have constructed various kinds of universal domains. We present here a categorical generalization of a well-known result in model theory, which we use to characterize large classes of reasonable categories that contain universal homogeneous objects. The existence of such objects is characterized by the condition that the finite objects in the category satisfy the amalgamation property. We derive from this the existence and uniqueness of universal homogeneous domains for several categories of bifinite domains, with embedding-projection-pairs as morphisms. We also obtain universal homogeneous objects for various categories of stable bifinite domains. In contrast, several categories of event domains and concrete domains and the category of all coherent Scott-domains do not contain universal homogeneous objects. Finally, we show that all our constructions can be performed effectively.

Type theory allows us to extract from a constructive proof that a specification is satisfiable a program that satisfies the specification. Algorithms for optimization of such programs are currently the object of research.

In this paper we consider one such algorithm, which was described in Beeson (1985) and which we will call ‘Harrop’. This algorithm greatly simplifies programs extracted from proofs in the Pure Construction Calculus. We use a Partial Equivalence Relation model for higher order lambda calculus, to check that t and Harrop(t) return the same outputs from the same inputs, i.e. that they are extensionally equal.

As a corollary, we show that it is correct (and, of course, useful) to replace a program t with Harrop(t). Such a correctness result has already been proved by Möhring (Möhring 1989a, 1989b) using realizability semantics, but we obtain it as a corollary of a new result, the extensional equality between t and Harrop(t). Also the semantic method we use is interesting in its own right.

We tackle the problems of correctness and efficiency of paralled implementations of functional languages. We present a compilation technique described in terms of program transformations in the functional framework. The original functional expression is transformed into a functional term, which can be seen as traditional machine code. The main feature of the parallel implementation is the use of continuations. We introduce a parallel abstract machine describing lazy task creation in terms of exportation of continuations. The advantages of the approach are twofold: (1)correetness proofs are made simpler and (2) the implementation is efficient because the use of continuations reduces the task management overhead.

Category theory offers a unified mathematical framework for the study of specifications and programs in a variety of styles, such as procedural, functional and concurrent. One way that these different languages may be treated uniformly is by generalising the definitions of some standard categorical concepts. In this paper we reproduce in the generalised theory analogues of some standard theorems on isomorphism, and outline their applications to programming languages.

Least fixpoints are constructed for finite coproducts of definable endofunctors of Cartesian closed categories that have weak polynomial products and joint equalizers of arbitrary families of pairs of parallel arrows. Both conditions hold in PER, the category whose objects are partial equivalence relations on N, and whose arrows are partial recursive functions. Weak polynomial products exist in any cartesian closed category with a finite number of objects as well as in any model of second order polymorphic lambda calculus: that is, in the proof theory of any second order positive intuitionistic propositional calculus, but such a category need not have equalizers. 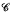However, any finite coproduct of definable endofunctors of a cartesian closed category with weak polynomial products will have a least fixpoint in a larger category 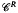with equalizers whose objects are right ideals (or sieves) of modulo certain congruence relations, and whose arrows are induced from .

In this article, we indicate how the category theoretical approach to tree automata, due to Betti and Kasangian, can be fruitfully combined with Walters’ categorical approach to context-free grammars to provide a simple way of establishing the well-known correspondence between context-free languages and the behaviors of non-deterministic tree automata. The connecting link between the two notions is provided by the theory of relational presheaves.

Equational deduction is generalised within a category-based abstract model theory framework, and proved complete under a hypothesis of quantifier projectivity, using a semantic treatment that regards quantifiers as models rather than variables, and valuations as model morphisms rather than functions. Applications include many- and order-sorted (conditional) equational logics, Horn clause logic, equational deduction modulo a theory, constraint logics, and more, as well as any possible combination among them. In the cases of equational deduction modulo a theory and of constraint logic the completeness result is new. One important consequence is an abstract version of Herbrand's Theorem, which provides an abstract model theoretic foundation for equational and constraint logic programming.

The categorical dual construction of initial abstract data types is studied. The resulting terminal co-algebras represent not only an implementation independent semantics of infinite objects such as streams, but also a suitable formal basis for object types in the sense of the object-oriented programming paradigm. Instances of object types may be interpreted as abstract automata with several state transition functions representing the methods of an object, and several output functions representing the attributes. By structuring the index set of the possibly infinite family of methods, and by structuring the output set, one can specify specific object types. For dealing simultaneously with complex data types and object types, it is not necessary to live within a cartesian closed category. In ccc's there are standard functional constructions for object types, but object types are not necessarily a higher-order construction. A world of data types and object types may be combined with the Rewriting Logic of Meseguer to obtain a formal basis for concurrent object systems.

An analysis of relationships between Craig-style interpolation, compactness, and other related model-theoretic properties is carried out in the softer framework of categories of pre-institutions. While the equivalence between sentence interpolation and the Robinson property under compactness and Boolean closure is well known, a similar result under different assumptions (not involving compactness) is newly established for presentation interpolation. The standard concept of naturality of model transformation is enriched by a new property, termed restriction adequacy, which proves useful for the reduction of interpolation along pre-institution transformations. A distinct reduction theorem for the Robinson property is presented as well. A variant of the ultraproduct concept is further introduced, and the related closure property for pre-institutions is shown to be equivalent to compactness

The subject of linear logic has recently become very important in theoretical computer science. It is apparent that the *-autonomous categories studied at length in by Barr (1979) are a model for a large fragment of linear logic, although not quite for the whole thing. Since the main reference is out of print and since large parts of that volume are devoted to results highly peripheral to the matter at hand, it seemed reasonable to provide a short introduction to the subject.