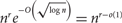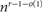Refine search
Actions for selected content:
48532 results in Computer Science
13 - The Normal Distribution
- from Part V - Advanced Topics
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 293-315
-
- Chapter
- Export citation
15 - Convolutional Neural Networks
- from Part V - Advanced Topics
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 333-364
-
- Chapter
- Export citation
List of Abbreviations
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp xiv-xv
-
- Chapter
- Export citation
6 - Fisher’s Linear Discriminant
- from Part II - Domain-Independent Feature Extraction
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 123-140
-
- Chapter
- Export citation
Contents
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp v-x
-
- Chapter
- Export citation
List of Tables
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp xi-xii
-
- Chapter
- Export citation
8 - Probabilistic Methods
- from Part III - Classifiers and Tools
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 173-195
-
- Chapter
- Export citation
Part IV - Handling Diverse Data Formats
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 243-244
-
- Chapter
- Export citation
1 - Introduction
- from Part I - Fundamental Theories
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 3-12
-
- Chapter
- Export citation
Notation
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp xvi-xvi
-
- Chapter
- Export citation
5 - Robust Speaker Verification
- from Part II - Advanced Studies
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 169-216
-
- Chapter
- Export citation
8 - Future Direction
- from Part II - Advanced Studies
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 266-275
-
- Chapter
- Export citation
References
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 289-306
-
- Chapter
- Export citation
1 - Introduction
- from Part I - Introduction and Overview
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 3-14
-
- Chapter
- Export citation
Part I - Introduction and Overview
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 1-2
-
- Chapter
- Export citation
Appendix - Exercises
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 276-288
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 365-378
-
- Chapter
- Export citation
6 - Domain Adaptation
- from Part II - Advanced Studies
-
- Book:
- Machine Learning for Speaker Recognition
- Published online:
- 26 June 2020
- Print publication:
- 19 November 2020, pp 217-248
-
- Chapter
- Export citation
Plates
-
- Book:
- Essentials of Pattern Recognition
- Published online:
- 08 December 2020
- Print publication:
- 19 November 2020, pp 385-400
-
- Chapter
- Export citation
Generalizations of the Ruzsa–Szemerédi and rainbow Turán problems for cliques
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 19 November 2020, pp. 591-608
-
- Article
-
- You have access
- Open access
- Export citation