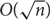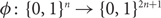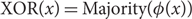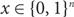Refine search
Actions for selected content:
48532 results in Computer Science
Backjumping is Exception Handling
-
- Journal:
- Theory and Practice of Logic Programming / Volume 21 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 125-144
-
- Article
-
- You have access
- Open access
- Export citation
Lipschitz bijections between boolean functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 513-525
-
- Article
- Export citation
ROB volume 38 issue 12 Cover and Back matter
-
- Article
-
- You have access
- Export citation
A simple differential geometry for complex networks
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. S106-S133
-
- Article
- Export citation
ANALYTICAL RESULTS ON THE SERVICE PERFORMANCE OF STOCHASTIC CLEARING SYSTEMS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 November 2020, pp. 217-236
-
- Article
- Export citation
A MEAN FIELD GAME ANALYSIS OF SIR DYNAMICS WITH VACCINATION
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 November 2020, pp. 482-499
-
- Article
- Export citation

A First Course in Random Matrix Theory
- for Physicists, Engineers and Data Scientists
-
- Published online:
- 12 November 2020
- Print publication:
- 03 December 2020
Index
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 267-270
-
- Chapter
- Export citation
10 - Lower Bounds for Summaries
- from Part II - Advanced Summaries and Extensions
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 242-252
-
- Chapter
- Export citation
4 - Summaries for Ordered Data
- from Part I - Fundamental Summary Techniques
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 120-150
-
- Chapter
- Export citation
2 - Summaries for Sets
- from Part I - Fundamental Summary Techniques
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 29-67
-
- Chapter
- Export citation
Contents
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp v-vii
-
- Chapter
- Export citation
8 - Summaries over Distributed Data
- from Part II - Advanced Summaries and Extensions
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 207-217
-
- Chapter
- Export citation
3 - Summaries for Multisets
- from Part I - Fundamental Summary Techniques
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 68-119
-
- Chapter
- Export citation
Part II - Advanced Summaries and Extensions
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 151-152
-
- Chapter
- Export citation
7 - Graph Summaries
- from Part II - Advanced Summaries and Extensions
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 192-206
-
- Chapter
- Export citation
Measuring the strength of threats, rewards, and appeals in persuasive negotiation dialogues
-
- Journal:
- The Knowledge Engineering Review / Volume 35 / 2020
- Published online by Cambridge University Press:
- 12 November 2020, e36
-
- Article
- Export citation
References
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 253-266
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp i-iv
-
- Chapter
- Export citation
Part I - Fundamental Summary Techniques
-
- Book:
- Small Summaries for Big Data
- Published online:
- 22 October 2020
- Print publication:
- 12 November 2020, pp 27-28
-
- Chapter
- Export citation