Refine search
Actions for selected content:
25794 results in Abstract analysis
Free products of inverse semigroups II
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 373-387
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
Unique factorization in Cayley arithmetics and cryptology
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 267-273
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
The distribution of cube-full numbers
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 287-295
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
Goldie criteria for some semiprime rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 297-308
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
On the construction of matrix representations and their extensions II
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 323-341
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
GMJ volume 33 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
Topological invariants of weighted homogeneous polynomials
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-245
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
An embedding for π2 of a subcomplex of a finite contractible two-complex
-
- Journal:
- Glasgow Mathematical Journal / Volume 33 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 18 May 2009, pp. 365-371
- Print publication:
- September 1991
-
- Article
-
- You have access
- Export citation
1 - Preliminaries
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 1-15
-
- Chapter
- Export citation
3 - Unbounded derivations
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 55-100
-
- Chapter
- Export citation
Preface
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp ix-xii
-
- Chapter
- Export citation
4 - C*-dynamical systems
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 101-207
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp i-vi
-
- Chapter
- Export citation
Contents
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp vii-viii
-
- Chapter
- Export citation
References
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 207-216
-
- Chapter
- Export citation
Index
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 217-219
-
- Chapter
- Export citation
2 - Bounded derivations
-
- Book:
- Operator Algebras in Dynamical Systems
- Published online:
- 27 March 2010
- Print publication:
- 30 August 1991, pp 16-54
-
- Chapter
- Export citation
Chapter 5 - Dirac operators and manifolds
-
- Book:
- Clifford Algebras and Dirac Operators in Harmonic Analysis
- Published online:
- 23 November 2009
- Print publication:
- 26 July 1991, pp 247-320
-
- Chapter
- Export citation
Index
-
- Book:
- Clifford Algebras and Dirac Operators in Harmonic Analysis
- Published online:
- 23 November 2009
- Print publication:
- 26 July 1991, pp 328-334
-
- Chapter
- Export citation
Chapter 1 - Clifford algebras
-
- Book:
- Clifford Algebras and Dirac Operators in Harmonic Analysis
- Published online:
- 23 November 2009
- Print publication:
- 26 July 1991, pp 5-86
-
- Chapter
- Export citation
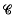 be the classical Cayley algebra defined over the reals with basis
be the classical Cayley algebra defined over the reals with basis 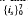 where
where 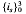 gives a quaternion algebra ℋ
gives a quaternion algebra ℋ
