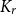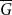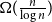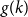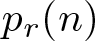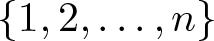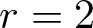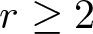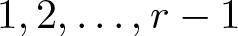Refine search
Actions for selected content:
25841 results in Abstract analysis

Dilation and Model Theory for Pairs of Commuting Contraction Operators
- Coming soon
-
- Expected online publication date:
- July 2026
- Print publication:
- 31 July 2026
-
- Book
- Export citation

A Primer, and Beyond, on Composition Operators on the Unit Disk
- Coming soon
-
- Expected online publication date:
- June 2026
- Print publication:
- 30 June 2026
-
- Book
- Export citation

Weak Solutions to Gradient Flows in Metric Measure Spaces
- Coming soon
-
- Expected online publication date:
- April 2026
- Print publication:
- 30 April 2026
-
- Book
- Export citation

Spectra of Discrete Structures
- Coming soon
-
- Expected online publication date:
- March 2026
- Print publication:
- 31 March 2026
-
- Book
- Export citation
Average sizes of mixed character sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESIDUES OF INTERTWINING OPERATORS FOR HEISENBERG PARABOLIC SUBGROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-214
-
- Article
- Export citation
Superlinear problems involving nonlinear superposition operators of mixed fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2026, pp. 1-26
-
- Article
- Export citation
Clique density vs blowups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 22 January 2026, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BEAUVILLE–LASZLO GLUING OF ALGEBRAIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 21 January 2026, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRISMATIC COHOMOLOGY OF RIGID ANALYTIC SPACES OVER DE RHAM PERIOD RING
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 January 2026, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviours of multiscale multivalued stochastic systems with small noises
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2026, pp. 1-57
-
- Article
- Export citation
Multivariate multifractal analysis of Lévy functions. Part I: Determination of multifractal spectra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-32
-
- Article
- Export citation
THE LOCAL/LOGARITHMIC CORRESPONDENCE AND THE DEGENERATION FORMULA FOR QUASIMAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Competition of small targets in planar domains: from Dirichlet to Robin and Steklov boundary condition
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ground states of the planar nonlinear Schrödinger–Newton system with a point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-26
-
- Article
- Export citation
Rigidity for the heat equation with density on Riemannian manifolds through a conformal change
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-41
-
- Article
- Export citation
A note on time-asymptotic bounds with a sharp algebraic rate and a transitional exponent for the sublinear Fujita problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2026, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enriched cycle structures and roots of permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 January 2026, pp. 1-18
-
- Article
- Export citation
Axisymmetric stationary surfaces for the moment of inertia
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 January 2026, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adversarial robustness of artificial intelligence
-
- Journal:
- European Journal of Applied Mathematics / Volume 37 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 06 January 2026, pp. 1-2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation