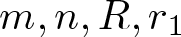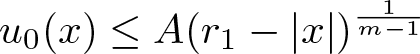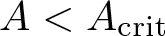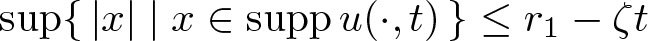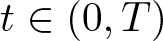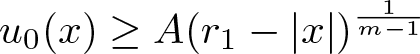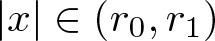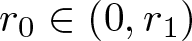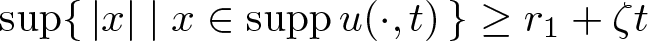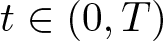Refine search
Actions for selected content:
25814 results in Abstract analysis
Log geometric models for little disks operads in even dimensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random embeddings of bounded-degree trees with optimal spread
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beyond the broken tetrahedron
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-12
-
- Article
- Export citation
EXCEPTIONAL PAIRS ON DEL PEZZO SURFACES AND SPACES OF COMPATIBLE FEIGIN-ODESSKII BRACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-35
-
- Article
- Export citation
Quantitative quasi-invariance of Gaussian measures below the energy level for the 1D generalized nonlinear Schrödinger equation and application to global well-posedness
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-33
-
- Article
- Export citation
DENOMINATORS IN LUSZTIG’S ASYMPTOTIC HECKE ALGEBRA VIA THE PLANCHEREL FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Saturation in random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The complexity of intersecting subproducts with subgroups in Cartesian powers
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterization of some convex curves on the 3-sphere
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-21
-
- Article
- Export citation
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in
 $\mathbb{C}^2$
$\mathbb{C}^2$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomologies, deformations and abelian extensions of Lie super triple systems with superderivations
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-22
-
- Article
- Export citation
Weighted Lipschitz shadowing and generalized weighted limit shadowing for infinite-dimensional systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-39
-
- Article
- Export citation
On the non-properness set of a local homeomorphism
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-15
-
- Article
- Export citation
Shrinking vs. expanding: the evolution of spatial support in degenerate Keller–Segel systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric Hom–Leibniz algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-24
-
- Article
- Export citation
Schwartz very weak solutions for Schrödinger type equations with distributional coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit spectral gap for Hecke congruence covers of arithmetic Schottky surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-41
-
- Article
- Export citation
Equilibrium and non-equilibrium diffusion approximation for the radiative transfer equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPHERE-LIKE ISOPARAMETRIC HYPERSURFACES IN DAMEK–RICCI SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on twisted moments of Dirichlet
 $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation