Refine search
Actions for selected content:
25801 results in Abstract analysis
The zeros of a certain family of trinomials
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-74
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
The spectral theory of second order two-point differential operators: I. A priori estimates for the eigenvalues and completeness
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 279-301
- Print publication:
- 1992
-
- Article
- Export citation
Asymptotic behaviour of solutions to the coagulation–fragmentation equations. I. The strong fragmentation case
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 231-244
- Print publication:
- 1992
-
- Article
- Export citation
Initial boundary value problems for isentropic gas dynamics
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-23
- Print publication:
- 1992
-
- Article
- Export citation
Homogenisation of parametrised families of hyperbolic problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 199-221
- Print publication:
- 1992
-
- Article
- Export citation
PRM volume 122 issue 3-4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
Piecewise continuous solutions of nonlinear pseudoparabolic equations in two space dimensions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 203-217
- Print publication:
- 1992
-
- Article
- Export citation
PRM volume 122 issue 1-2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
GMJ volume 34 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
Existence and boundedness of a minimiser for a constrained minimisation problem on Rn with limiting exponent
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 221-235
- Print publication:
- 1992
-
- Article
- Export citation
PRM volume 121 issue 3-4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
Existence of positive entire solutions for weakly coupled semilinear elliptic systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 79-91
- Print publication:
- 1992
-
- Article
- Export citation
Centers of mass for operator-families
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-126
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
Cardinal interpolation with shifted three-directional box splines†
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 205-220
- Print publication:
- 1992
-
- Article
- Export citation
Function spaces related to gauge groups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 185-190
- Print publication:
- 1992
-
- Article
- Export citation
Exponential length and exponential rank in C*-algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 55-71
- Print publication:
- 1992
-
- Article
- Export citation
Water waves for small surface tension: an approach via normal form
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 267-299
- Print publication:
- 1992
-
- Article
- Export citation
Universal notions characterizing spectral decompositions
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 109-116
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
Index to Volume 121
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 381-382
- Print publication:
- 1992
-
- Article
- Export citation
Transitive flows: a semi-group approach
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 348-361
- Print publication:
- December 1991
-
- Article
- Export citation
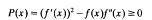
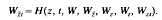
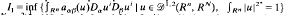 where
where 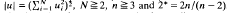 . We also prove the boundedness of the minimiser of
. We also prove the boundedness of the minimiser of 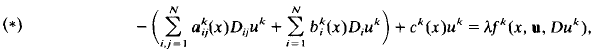
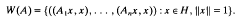
 is close to 1. The Bond number
is close to 1. The Bond number 

