Refine search
Actions for selected content:
25813 results in Abstract analysis
Characterisation of the factors of quasi-differential expressions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 297-312
- Print publication:
- 1992
-
- Article
- Export citation
Initial conditions for integrable-square solutions to singular differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 117-127
- Print publication:
- 1992
-
- Article
- Export citation
Interpolating sequences for the derivatives of Bloch functions
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-41
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
Integral closures of ideals relative to Artinian modules, and exact sequences
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-107
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
On the domains of minimal and maximal operators for regularisable singular differential expressions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 191-202
- Print publication:
- 1992
-
- Article
- Export citation
On the geometry of the unit spheres of the Lorentz spaces Lw,1
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-25
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
A priori bounds for solutions of an elliptic equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 191-204
- Print publication:
- 1992
-
- Article
- Export citation
A centre manifold theorem for hyperbolic PDEs
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 363-377
- Print publication:
- 1992
-
- Article
- Export citation
Differentiable functions on algebras and the equation grad (w) = M grad (v)
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 353-361
- Print publication:
- 1992
-
- Article
- Export citation
On a Ramanujan's identity
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 17-19
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
Stochastic reinforcement problems and ergodic theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 33-53
- Print publication:
- 1992
-
- Article
- Export citation
PRM volume 121 issue 3-4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
PRM volume 122 issue 3-4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
PRM volume 121 issue 1-2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
PRM volume 120 issue 3-4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1992
-
- Article
-
- You have access
- Export citation
On the number of terms in the irreducible factors of a polynomial over ℚ
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-15
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
The validity of modulation equations for extended systems with cubic nonlinearities
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 85-91
- Print publication:
- 1992
-
- Article
- Export citation
A structure theorem for SI-Modules
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 83-89
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
The group of homotopy self-equivalences of non-simply-connected spaces using Postnikov decompositions II1
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 127-135
- Print publication:
- 1992
-
- Article
- Export citation
On the stochastic nonlinear neutron transport equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 253-272
- Print publication:
- 1992
-
- Article
- Export citation
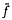 acting on the Bergman space is shown to be equivalent to
acting on the Bergman space is shown to be equivalent to 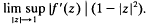 .
.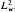 , for the regularised expression, coincide with the corresponding domains for the expression in its original, singular form.
, for the regularised expression, coincide with the corresponding domains for the expression in its original, singular form.
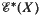 . This group extension sequence gives
. This group extension sequence gives 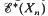 in terms of
in terms of 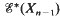 , where
, where 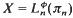 is the generalised Eilenberg–McLane space corresponding to the action ϕ: π
is the generalised Eilenberg–McLane space corresponding to the action ϕ: π