Refine search
Actions for selected content:
25813 results in Abstract analysis
Quantum stochastic integrals as belated integrals
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 165-173
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Regular graphs with regular neighborhoods
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 215-218
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Index to Volume 122
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 379-380
- Print publication:
- 1992
-
- Article
- Export citation
Global stability in models of population dynamics with diffusion. I. Patchy environments
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 69-84
- Print publication:
- 1992
-
- Article
- Export citation
Periodic homogenisation of certain fully nonlinear partial differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 245-265
- Print publication:
- 1992
-
- Article
- Export citation
The resolvent problem for the Stokes system in exterior domains: uniqueness and non-regularity in Hölder spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-10
- Print publication:
- 1992
-
- Article
- Export citation
Multiple bifurcation in a predator–prey system with nonmonotonic predator response
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 313-347
- Print publication:
- 1992
-
- Article
- Export citation
A note on lower limit of series and potential theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 273-277
- Print publication:
- 1992
-
- Article
- Export citation
Existence of multiple positive solutions for a semilinear equation with critical exponent*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 161-175
- Print publication:
- 1992
-
- Article
- Export citation
Uniform asymptotic expansions for oblate spheroidal functions I: positive separation parameter λ
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 303-320
- Print publication:
- 1992
-
- Article
- Export citation
On a class of QI-rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 75-81
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
The
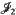 -radical in structural matrix near rings, II
-radical in structural matrix near rings, II
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 53-61
- Print publication:
- 1992
-
- Article
- Export citation
A global estimate for the gradient in a singular elliptic boundary value problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 341-352
- Print publication:
- 1992
-
- Article
- Export citation
The semigroup of continuous selfmaps of I has infinitely many ideals
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 27-33
- Print publication:
- January 1992
-
- Article
-
- You have access
- Export citation
A note on primeness of semigroup rings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 191-197
- Print publication:
- 1992
-
- Article
- Export citation
Remark on the Dirichlet problem for harmonic maps from the disc into the 2-sphere
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 63-67
- Print publication:
- 1992
-
- Article
- Export citation
On the growth of the relative volume of a tube with its radius*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 255-265
- Print publication:
- 1992
-
- Article
- Export citation
Robustness of a feedback control scheme for one-dimensional diffusion equations: perturbation to the Sturm-Liouville operator
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 121 / Issue 3-4 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 349-359
- Print publication:
- 1992
-
- Article
- Export citation
The exact coupled bounds for effective tensors of electrical and magnetic properties of two-component two-dimensional composites1
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 122 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 93-125
- Print publication:
- 1992
-
- Article
- Export citation
On periodic solutions for singular perturbation problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 120 / Issue 1-2 / 1992
- Published online by Cambridge University Press:
- 14 November 2011, pp. 143-152
- Print publication:
- 1992
-
- Article
- Export citation
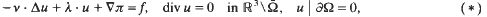
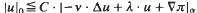 for
for 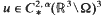 with
with 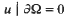 , div
, div 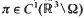 with
with 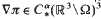 . However, if a solution (
. However, if a solution (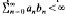 , then
, then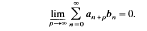
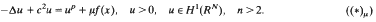
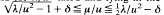 when 1 = 1≦λ/u
when 1 = 1≦λ/u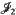 -radical in structural matrix near rings, II
-radical in structural matrix near rings, II
 (
(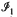 and
and