Refine search
Actions for selected content:
25814 results in Abstract analysis
Kac modules of sl (2/2) and the extended Kac-Weyl formulas
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-48
- Print publication:
- June 1992
-
- Article
- Export citation
Random polytopes in smooth convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-92
- Print publication:
- June 1992
-
- Article
- Export citation
Oscillations of solutions of general integrodifferential equations
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 152-160
- Print publication:
- June 1992
-
- Article
- Export citation
MTK volume 39 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
A note on the Krull dimension of certain algebras
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
- Print publication:
- June 1992
-
- Article
- Export citation
The spectral theory of multiplication operators and the recurrence properties for nondifferentiable functions in the Zygmund class Λ*a
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-151
- Print publication:
- June 1992
-
- Article
- Export citation
A note on the joint operator norm of hermitian operators on Banach spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 219-220
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
The regular radical of semigroup rings of commutative semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 133-141
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
The Mazur property and completeness in the space of Bochner-integrable functions L1(μ, X)
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 201-206
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Extending Edgar's ordering to locally convex spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 175-188
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Homological characterizations of the approximation property for Banach spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 229-239
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Homotopy of compact symmetric spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-228
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Partial Gaussian sums III
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 253-261
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
The essential norms of composition operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 143-155
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
On the Hirsch-Plotkin radical of a factorized group
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-199
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Bounded endomorphisms of free P-algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 209-214
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
A functorial approach to weak amenability for commutative Banach algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-251
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
GMJ volume 34 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Unbounded approximate identities in normed algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 189-192
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
Some p-algebras and double p-algebras having only principal congruences
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-164
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation
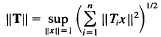
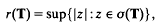
 ) has the
) has the