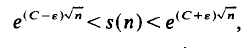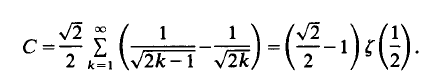Refine search
Actions for selected content:
25814 results in Abstract analysis
Contents
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp vii-x
-
- Chapter
- Export citation
IX - Jensen's Formula Again
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp 1-157
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp i-vi
-
- Chapter
- Export citation
X - Why we want to have multiplier theorems
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp 158-297
-
- Chapter
- Export citation
Foreword to volume II, with an example for the end of volume I
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp xi-xxiv
-
- Chapter
- Export citation
Errata for volume I
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp xxv-xxvi
-
- Chapter
- Export citation
Index
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp 572-574
-
- Chapter
- Export citation
Bibliography for volume II
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp 566-571
-
- Chapter
- Export citation
XI - Multiplier theorems
-
- Book:
- The Logarithmic Integral
- Published online:
- 07 January 2010
- Print publication:
- 20 August 1992, pp 298-565
-
- Chapter
- Export citation
Euclidean representations of topologically ordered spaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-135
- Print publication:
- June 1992
-
- Article
- Export citation
The bisectrix of a tetrahedron
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-103
- Print publication:
- June 1992
-
- Article
- Export citation
Minimal length functions on groups
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-61
- Print publication:
- June 1992
-
- Article
- Export citation
On Bombieri and Davenport's theorem concerning small gaps between primes
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-17
- Print publication:
- June 1992
-
- Article
- Export citation
σ-fragmentable Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-188
- Print publication:
- June 1992
-
- Article
- Export citation
On some intermediate rings
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-66
- Print publication:
- June 1992
-
- Article
- Export citation
The volume of duals and sections of polytopes
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-80
- Print publication:
- June 1992
-
- Article
- Export citation
An asymptotic formula for a-th powers dividing binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
- Print publication:
- June 1992
-
- Article
- Export citation
Simultaneous additive congruences to a large prime modulus
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1992
-
- Article
- Export citation
T-numbers form an M0 set
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-24
- Print publication:
- June 1992
-
- Article
- Export citation
D. J. Albers, G. L. Alexanderson and C. Reid. Editors. More Mathematical People: Contemporary Conversations. Harcourt Brace Jovanovich. 1990, 375 pp., 231 illustrations, $29.95. - R. J. Baston and M. G. Eastwood. The Penrose Transform. Clarendon Press. 1989, 213 pp., £25. - A. Bejancu. Finsler Geometry and Applications. Ellis Horwood. 1990, 195 pp., £35 - C. A. Berenstein and R. Gay. Complex Variables: An Introduction. Springer. 1991, 665 pp., DM128. - F. A. Berezin and M. A. Shubin. The Schrödinger Equation. Kluwer. 1991, 555 pp., £136. - M. Black. Harmonic Maps into Homogeneous Spaces. Longman. 1991, 92 pp., £14. - W. C. Brown. Matrices and Vector Spaces. Marcel Dekker. 1991, 328 pp., $49.75. - P. M. Cohn. Algebraic Numbers and Algebraic Functions. Chapman and Hall. 1991, 192 pp., £25. - H. T. Croft, K. J. Falconer and R. K. Guy. Unsolved Problems in Geometry. Springer. 1991, 198 pp., DM84. - D. A. Dubin and M. A. Hennings. Quantum Mechanics, Algebras and Distributions. Longman. 1990, 238 pp., £19·50. - G. A. Edgar. Measure, Topology and Fractal Geometry. Springer. 1989, 230 pp., DM58. - L. Evens. The Cohomology of Groups. Clarendon Press. 1991, 159 pp., £20. - M. Faierman. Two-parameter Eigenvalue Problems in Ordinary Differential Equations. Longman. 1991, 160 pp., £17. - P. A. Firby and C. F. Gardiner. Surface Topology, 2nd Edition. Ellis and Horwood. 1991, 220 pp., £18·99. - I. Frenkel, J. Lepowsky and A. Meurman. Vertex Operator Algebras and the Monster. Academic Press. 1989, 508 pp., $69.95. - R. V. Gamkrelidze. Editor. Analysis II. Springer. 1990, 255 pp., DM128. - L. Györi and G. Ladas. Oscillation Theory of Delay Differential Equations with Applications. Clarendon Press. 1991, 368 pp., £45. - A. J. Hahn and O. T. O'Meara. The Classical Groups and K-Theory. Springer. 1989, 565 pp., DM198. - L. Hörmander. The Analysis of Linear Partial Differential Operators I, 2nd edition. Springer. 1990, 440 pp., DM69. - J. M. Howie. Automata and Languages. Clarendon Press. 1991, 294 pp., £15. - A. Isaacs, J. Daintith and E. Martin. Editors. The Oxford Dictionary for Scientific Writers and Editors. Clarendon Press. 1991, 389 pp., £14·95 - H. Lauwerier. Fractals. Penguin Books. 1991, 210 pp., £9·99. - S. G. Mikhlin. Error Analysis in Numerical Process. Wiley. 1991, 283 pp., £39. - R. S. Millman and G. D. Parker. Geometry: a Metric Approach with Models, 2nd edition. Springer. 1991, 370 pp., DM98. - D. Y. Petrina, V. I. Gerasimenko and P. V. Malyshev. Mathematical Foundations of Classical Statistical Mechanics (Continuous Systems). Gordon and Breach. 1989, 338 pp., $198. - M. M. Rao and Z. D. Ren. Theory of Orlicz Spaces. Marcel Dekker. 1991, 472 pp., $166.75. - R. Remmert. Theory of Complex Functions. Springer. 1990, 440 pp., DM118. - B. L. Sendov. Hausdorff Approximations. Kluwer. 1990, 364 pp., £81. - K. L. Teo, C. J. Goh and K. H. Wong. A Unified Computational Approach to Optimal Control Problems. Longman. 1991, 326 pp., £46. - S. G. Vladut. Kronecker's Jugendtraum and Modular Functions. Gordon and Breach. 1991, 411 pp., £46. - D. Wells. The Penguin Dictionary of Curious and Interesting Geometry. Penguin Books. 1991, 285 pp., £10·99 or $20.00. - A. Weil. Number Theory: An Approach through History; from Hammurabi to Legendre. Birkhäuser. 1984, 375 pp., 17 illustrations, £50·25. - A. Weil. The Apprenticeship of a Mathematician. Birkhäuser. 1992, 197 pp., 58 Swiss Francs. - Xiaolu Wang. The C*-algebras of a Class of Solvable Lie Groups. Longman. 1989, 127 pp., £14·50.
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-196
- Print publication:
- June 1992
-
- Article
- Export citation
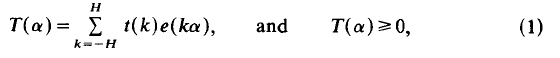
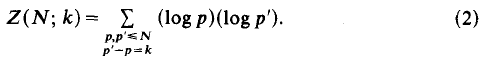

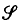 is any family of subsets of
is any family of subsets of 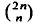 satisfies for arbitrary
satisfies for arbitrary