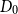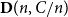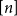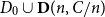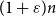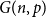Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
Symbol index
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 283-284
-
- Chapter
- Export citation
5 - Examples from the social sciences
- from Part II - Tangles in Different Contexts
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 41-52
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp v-viii
-
- Chapter
- Export citation
Notes
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 251-272
-
- Chapter
- Export citation
Part II - Tangles in Different Contexts
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 31-32
-
- Chapter
- Export citation
Part IV - Applying Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 185-186
-
- Chapter
- Export citation
13 - Applying tangles in the social sciences
- from Part IV - Applying Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 203-214
-
- Chapter
- Export citation
Index
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 277-282
-
- Chapter
- Export citation
Part III - The Mathematics of Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 73-74
-
- Chapter
- Export citation
3 - The two main tangle theorems: an informal preview
- from Part I - Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 27-30
-
- Chapter
- Export citation
12 - Applying tangles in the natural sciences
- from Part IV - Applying Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 187-202
-
- Chapter
- Export citation
2 - The notion of a tangle
- from Part I - Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 15-26
-
- Chapter
- Export citation
6 - Examples from data science
- from Part II - Tangles in Different Contexts
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 53-72
-
- Chapter
- Export citation
1 - The idea behind tangles
- from Part I - Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 3-14
-
- Chapter
-
- You have access
- Export citation
4 - Examples from the natural sciences
- from Part II - Tangles in Different Contexts
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 33-40
-
- Chapter
- Export citation
10 - Choosing the feature system
- from Part III - The Mathematics of Tangles
-
- Book:
- Tangles
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 157-168
-
- Chapter
- Export citation

Tangles
- A Structural Approach to Artificial Intelligence in the Empirical Sciences
-
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024
Rainbow Hamiltonicity in uniformly coloured perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 624-642
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum chordal subgraphs of random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 03 May 2024, pp. 611-623
-
- Article
- Export citation