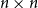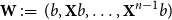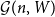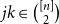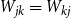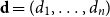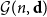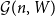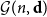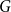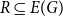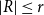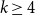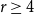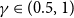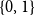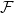Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
2 - Steiner Systems
-
- Book:
- The Art of Working with the Mathieu Group M24
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 6-16
-
- Chapter
- Export citation
Expansion of the critical intensity for the random connection model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 November 2024, pp. 158-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

The Art of Working with the Mathieu Group M24
-
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 115-130
-
- Article
- Export citation
Sampling repulsive Gibbs point processes using random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vertex-critical graphs far from edge-criticality
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximation of subgraph counts in the uniform attachment model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 90-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on extremal constructions for the Erdős–Rademacher problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 52-62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 October 2024, pp. 1-51
-
- Article
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The List-Ramsey threshold for families of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 829-851
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new formula for the determinant and bounds on its tensor and Waring ranks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 769-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 795-806
-
- Article
- Export citation
On the Ramsey numbers of daisies II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 742-768
-
- Article
- Export citation
List packing number of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 807-828
-
- Article
- Export citation
Sublinear Expanders and Their Applications
-
-
- Book:
- Surveys in Combinatorics 2024
- Published online:
- 23 May 2024
- Print publication:
- 13 June 2024, pp 89-130
-
- Chapter
- Export citation
Transversals in Latin Squares
-
-
- Book:
- Surveys in Combinatorics 2024
- Published online:
- 23 May 2024
- Print publication:
- 13 June 2024, pp 131-158
-
- Chapter
- Export citation
Erdős Covering Systems
-
-
- Book:
- Surveys in Combinatorics 2024
- Published online:
- 23 May 2024
- Print publication:
- 13 June 2024, pp 31-54
-
- Chapter
- Export citation
Oriented Trees and Paths in Digraphs
-
-
- Book:
- Surveys in Combinatorics 2024
- Published online:
- 23 May 2024
- Print publication:
- 13 June 2024, pp 271-295
-
- Chapter
- Export citation