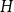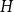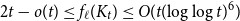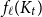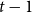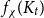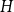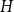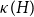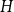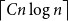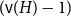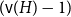Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
On the choosability of
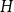 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
19 - Structure Constants
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 350-369
-
- Chapter
- Export citation
15 - Homogeneous Varieties
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 265-289
-
- Chapter
- Export citation
14 - Symplectic Schubert Polynomials
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 240-264
-
- Chapter
- Export citation
Appendix A - Algebraic Topology
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 370-387
-
- Chapter
- Export citation
2 - Defining Equivariant Cohomology
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 9-25
-
- Chapter
- Export citation
Preface
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp xi-xvi
-
- Chapter
- Export citation
11 - Degeneracy Loci
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 182-207
-
- Chapter
- Export citation
6 - Conics
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 79-92
-
- Chapter
- Export citation
9 - Schubert Calculus on Grassmannians
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 126-151
-
- Chapter
- Export citation
16 - The Algebra of Divided Difference Operators
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 290-310
-
- Chapter
- Export citation
17 - Equivariant Homology
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 311-325
-
- Chapter
- Export citation
8 - Toric Varieties
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 113-125
-
- Chapter
- Export citation
12 - Infinite-Dimensional Flag Varieties
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 208-225
-
- Chapter
- Export citation
Appendix C - Pfaffians and Q-polynomials
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 392-405
-
- Chapter
- Export citation
Appendix E - Characteristic Classes and Equivariant Cohomology
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 415-419
-
- Chapter
- Export citation
7 - Localization II
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 93-112
-
- Chapter
- Export citation
1 - Preview
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 1-8
-
- Chapter
- Export citation
13 - Symplectic Flag Varieties
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 226-239
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Equivariant Cohomology in Algebraic Geometry
- Published online:
- 07 October 2023
- Print publication:
- 26 October 2023, pp 435-446
-
- Chapter
- Export citation