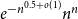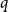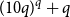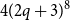Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
2 - What is Metadata?
-
- Chapter
- Export citation
Figures and Tables
-
- Chapter
- Export citation
Contents
-
- Chapter
- Export citation
Dedication
-
- Chapter
- Export citation
About the Authors
-
- Chapter
- Export citation
Acknowledgements
-
- Chapter
- Export citation
Introduction
-
- Chapter
- Export citation
Frontmatter
-
- Chapter
- Export citation
5 - Hello Halo Data
-
- Chapter
- Export citation
On the size of maximal intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 32-49
-
- Article
- Export citation
Forcing generalised quasirandom graphs efficiently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 05 September 2023, pp. 16-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation