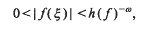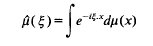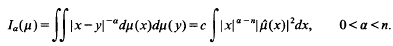Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
A sharp inequality related to Moser's inequality
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 357-366
- Print publication:
- December 1993
-
- Article
- Export citation
About four-ball packings
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 226-232
- Print publication:
- December 1993
-
- Article
- Export citation
Decomposition of sets of small or large boundary
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-304
- Print publication:
- December 1993
-
- Article
- Export citation
The large values of the Riemann Zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-214
- Print publication:
- December 1993
-
- Article
- Export citation
Asymptotic behaviour of orthogonal polynomials relative to measures with mass points
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-344
- Print publication:
- December 1993
-
- Article
- Export citation
Left orders in Abelian regular rings
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 256-274
- Print publication:
- December 1993
-
- Article
- Export citation
A. M. Anile, J. K. Hunter, P. Pantano and G. Russo. Ray methods for nonlinear waves in fluids and plasmas. Longman. 1993, 243pp., £39. - K. Arczewski and J. Pietrucha. Mathematical Modelling of Mechanical Complex Systems. Ellis Horwood. 1993, 293 pp., £45. - T. A. Bick. Elementary Boundary Value Problems. Marcel Dekker. 1993, 264 pp., $49.75. - P. Biler and T. Nadzieja. Problems and examples in differential equations. Marcel Dekker. 1992, 264 pp., $55. - W. C. Brown. Matrices over Commutative Rings. Marcel Dekker. 1993, 281pp., $115. - B. Choudhary. The Elements of Complex Analysis. 2nd Edition. Wiley Eastern. 1992, 325 pp., 85 Rupees. - J. R. Clay. Nearrings, Geneses and Applications. Oxford University Press. 1992, 469 pp., £55. - H. Davenport. The Higher Arithmetic. 6th Edition. Cambridge University Press. 1992, 217 pp., £12·95. - G. Evans. Practical Numerical Integration. Wiley. 1993, 328 pp., £37·95. - A. Fassler and E. Stiefel. Group Theoretical Methods and their Applications. Birkhauser. 1992, 296 pp., 98SFr. - J. Fauvel, R. Flood and R. Wilson, Editors. Möbius and his Band: Mathematics and Astronomy in Nineteenth Century Germany. Oxford University Press. 1993, 172 pp., £19·50. - G. H. Hardy. A Mathematician's Apology. Cambridge University Press. 1992, 153 pp., £4·95. - B. Makarov, M. G. Goluzina, A. A. Lodkin and A. N. Podkorytov. Selected Problems in Real Analysis. American Mathematical Society, 1992, 371 pp., £78. - J. E. Marsden. Lectures on Mechanics. Cambridge University Press. 1992, 254 pp., £19.95. - D. S. Mitrinovic, J. E. Pecaric and A. M. Fink. Classical and New Inequalities in Analysis. Kluwer Academic. 1993, 740 pp., £170·50. - K. W. Morton and M. J. Baines, Editors. Numerical Methods for Fluid Dynamics III. Clarendon Press. 1988, 529 pp., £50. - J. E. Munro. Discrete Mathematics. Chapman & Hall. 1992, 306 pp., £16·95. - C. Nash. Differential Topology and Quantum Field Theory. Academic Press. 1991, 386 pp., £27. - E. R. Pinch. Optimal Control and the Calculus of Variations. Oxford University Press. 1993, 234 pp., £35. - S. C. Power. Limit Algebras: an Introduction to Subalgebras of C*-algebras. Longman Scientific & Technical. 1992, 201 pp., £23. - C. Reutenauer. Free Lie Algebras. LMS Monographs New Series, No. 7. Clarendon Press. 1993, 269 pp., £55. - H. Triebel. Higher Analysis. J. A. Barth. 1992, 473 pp., DM 148. - N. E. Wegge-Olsen. K-Theory and C*-algebras, a friendly approach. Oxford University Press. 1993, 370 pp., £35. - G. C. Wen. Conformal Mappings and boundary value problems. American Mathematical Society. 1992, 303 pp., £68. - Yau Chuen Wong. Introductory Theory of Topological Vector Spaces. Marcel Dekker. 1992, 440 pp., $59·75.
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 375-380
- Print publication:
- December 1993
-
- Article
- Export citation
On the frequency distribution of partial quotients of U-numbers
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-225
- Print publication:
- December 1993
-
- Article
- Export citation
Estimates of spherial averages of Fourier transforms and dimensions of sets
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 322-330
- Print publication:
- December 1993
-
- Article
- Export citation
Determination of convex bodies by their brightness functions
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-168
- Print publication:
- December 1993
-
- Article
- Export citation
Sums and differences of quartic norms
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-245
- Print publication:
- December 1993
-
- Article
- Export citation
A short algebraic proof of a theorem of Warfield
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 275-277
- Print publication:
- December 1993
-
- Article
- Export citation
The volume of the intersection of a convex body with its translates
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-289
- Print publication:
- December 1993
-
- Article
- Export citation
Index to Volume 31–40
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 383-391
- Print publication:
- December 1993
-
- Article
- Export citation
5 - Semiaffine linear spaces with large order
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp 96-118
-
- Chapter
- Export citation
7 - d-Dimensional linear spaces
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp 136-166
-
- Chapter
- Export citation
Appendix
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp 189-211
-
- Chapter
- Export citation
Notation index
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp 212-212
-
- Chapter
- Export citation
Subject index
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp 213-214
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- The Theory of Finite Linear Spaces
- Published online:
- 05 May 2010
- Print publication:
- 26 November 1993, pp i-iv
-
- Chapter
- Export citation
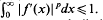 .
.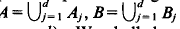 and vectors
and vectors 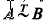 In [3], Theorem 3 we proved that if
In [3], Theorem 3 we proved that if 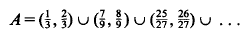
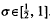 . By refining Selberg's method, we study the large values of
. By refining Selberg's method, we study the large values of 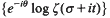 as
as 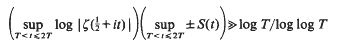
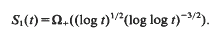
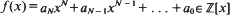 so that
so that