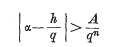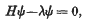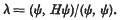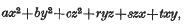Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Some Diophantine inequalities
-
- Journal:
- Mathematika / Volume 2 / Issue 2 / December 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-149
- Print publication:
- December 1955
-
- Article
- Export citation
On a method of Mordell in the geometry of numbers
-
- Journal:
- Mathematika / Volume 2 / Issue 2 / December 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-140
- Print publication:
- December 1955
-
- Article
- Export citation
The solubility of certain Diophantine inequalities
-
- Journal:
- Mathematika / Volume 2 / Issue 2 / December 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-96
- Print publication:
- December 1955
-
- Article
- Export citation
Rational approximations to algebraic numbers
-
- Journal:
- Mathematika / Volume 2 / Issue 2 / December 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 160-167
- Print publication:
- December 1955
-
- Article
- Export citation
Rational approximations to algebraic numbers
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-20
- Print publication:
- June 1955
-
- Article
-
- You have access
- Export citation
Duality in homotopy theory
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-80
- Print publication:
- June 1955
-
- Article
- Export citation
On the steady rotation of a sphere in a viscous fluid
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-47
- Print publication:
- June 1955
-
- Article
- Export citation
Sets of constant width contained in a set of given minimal width
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 48-55
- Print publication:
- June 1955
-
- Article
- Export citation
MTK volume 2 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1955
-
- Article
-
- You have access
- Export citation
Representation of integers by indefinite quadratic forms
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-38
- Print publication:
- June 1955
-
- Article
- Export citation
An elementary proof of Kato's lemma
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-41
- Print publication:
- June 1955
-
- Article
- Export citation
Witt groups and hyperexponential groups
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-31
- Print publication:
- June 1955
-
- Article
- Export citation
The Minkowski-Hlawka theorem
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-124
- Print publication:
- June 1954
-
- Article
- Export citation
On the steady motion of viscous liquid past a flat plate
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-156
- Print publication:
- June 1954
-
- Article
- Export citation
A two dimensional magnetic boundary layer problem
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-142
- Print publication:
- June 1954
-
- Article
- Export citation
Partial well-ordering of sets of vectors
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-95
- Print publication:
- June 1954
-
- Article
- Export citation
MTK volume 1 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1954
-
- Article
-
- You have access
- Export citation
A note on Stokes's stream-function for the slow steady motion of viscous fluid before plane and spherical boundaries
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-130
- Print publication:
- June 1954
-
- Article
- Export citation
On irregularities of distribution
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-79
- Print publication:
- June 1954
-
- Article
- Export citation
The representation of integers by positive ternary quadratic forms
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-110
- Print publication:
- June 1954
-
- Article
- Export citation