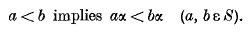Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
The p-adic generalization of the Thue-Siegel-Roth theorem
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-48
- Print publication:
- June 1958
-
- Article
- Export citation
MTK volume 5 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1958
-
- Article
-
- You have access
- Export citation
On sequences of integers
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-39
- Print publication:
- June 1958
-
- Article
- Export citation
The product of n linear forms in a field of series
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-137
- Print publication:
- December 1957
-
- Article
- Export citation
On the expansion of functions satisfying four boundary conditions
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-145
- Print publication:
- December 1957
-
- Article
- Export citation
The twisted sphere
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-165
- Print publication:
- December 1957
-
- Article
- Export citation
Rational approximations to algebraic numbers
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
- Print publication:
- December 1957
-
- Article
- Export citation
Cubic forms over algebraic number fields
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-101
- Print publication:
- December 1957
-
- Article
- Export citation
On a method for the determination of class number factors in number fields
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-121
- Print publication:
- December 1957
-
- Article
- Export citation
The relation between load and penetration for a spherical punch
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-161
- Print publication:
- December 1957
-
- Article
- Export citation
Index to volume 4
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, p. 169
- Print publication:
- December 1957
-
- Article
- Export citation
Note on two theorems about function algebras
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-139
- Print publication:
- December 1957
-
- Article
- Export citation
MTK volume 4 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
Homogeneous forms of odd degree in a large number of variables
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-105
- Print publication:
- December 1957
-
- Article
- Export citation
On the fractional parts of the powers of a rational number (II)
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
- Print publication:
- December 1957
-
- Article
- Export citation
On the solution of problems of dynamic plane elasticity
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 166-168
- Print publication:
- December 1957
-
- Article
- Export citation
An inversion formula for a generalized transform
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 146-155
- Print publication:
- December 1957
-
- Article
- Export citation
The distribution of quadratic residues and non-residues
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
- Print publication:
- December 1957
-
- Article
- Export citation
Groups of order automorphisms of ordered sets
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-50
- Print publication:
- June 1957
-
- Article
- Export citation
Uniqueness theorems for thin clamped anisotropic plates
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 70-75
- Print publication:
- June 1957
-
- Article
- Export citation
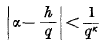
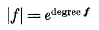
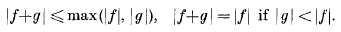
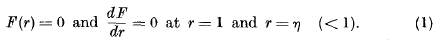

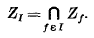
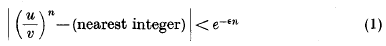
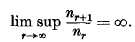
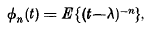
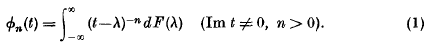
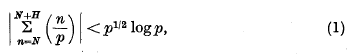
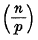 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.