Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
MTK volume 7 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
A metric for plane affine geometry over GF(2n)
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-148
- Print publication:
- December 1960
-
- Article
- Export citation
Convex semi-lattices of continuous functions
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-116
- Print publication:
- December 1960
-
- Article
- Export citation
Magneto-elastic wave propagation
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-171
- Print publication:
- December 1960
-
- Article
- Export citation
A combinatorial problem of T. G. Room
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-55
- Print publication:
- June 1960
-
- Article
- Export citation
Incidence matrices
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-49
- Print publication:
- June 1960
-
- Article
- Export citation
Distinct small values of quadratic forms
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-40
- Print publication:
- June 1960
-
- Article
- Export citation
The flow of a conducting fluid past a magnetized cylinder
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-77
- Print publication:
- June 1960
-
- Article
- Export citation
On Stokes flow about a torus
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-92
- Print publication:
- June 1960
-
- Article
- Export citation
The discriminants of relative extensions and the existence of integral bases
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-22
- Print publication:
- June 1960
-
- Article
- Export citation
A mixed packing problem
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-63
- Print publication:
- June 1960
-
- Article
- Export citation
MTK volume 7 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1960
-
- Article
-
- You have access
- Export citation
The stability of a rigidly rotating column of liquid
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1960
-
- Article
- Export citation
Symmetrically loaded shallow shells of revolution
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-35
- Print publication:
- June 1960
-
- Article
- Export citation
On infinitesimal triangles
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-14
- Print publication:
- June 1960
-
- Article
- Export citation
The genus field and genus group in finite number fields, II
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-146
- Print publication:
- December 1959
-
- Article
- Export citation
Index to volume 6
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, p. 165
- Print publication:
- December 1959
-
- Article
- Export citation
Cardinals of closed sets
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-107
- Print publication:
- December 1959
-
- Article
- Export citation
MTK volume 6 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1959
-
- Article
-
- You have access
- Export citation
The reduction number of a one-dimensional local ring
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-90
- Print publication:
- December 1959
-
- Article
- Export citation
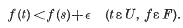
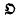 . We shall be concerned here with the structure of such rings
. We shall be concerned here with the structure of such rings 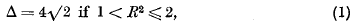
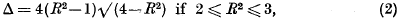
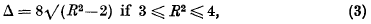
 , of K, which is defined as the maximal non-ramified extension of K composed of K and of some absolutely Abelian field.
, of K, which is defined as the maximal non-ramified extension of K composed of K and of some absolutely Abelian field.