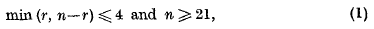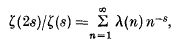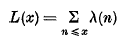Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
A note on the axially symmetrical punch problem*
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-119
- Print publication:
- December 1959
-
- Article
- Export citation
The receptance function of a beam
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-141
- Print publication:
- December 1959
-
- Article
- Export citation
On the solution of some axisymmetric boundary value problems by means of integral equations, II: further problems for a circular disc and a spherical cap
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-133
- Print publication:
- December 1959
-
- Article
- Export citation
The defect of a one-dimensional local ring
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
- Print publication:
- December 1959
-
- Article
- Export citation
Two centred expansion of the retarded Green's function
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-117
- Print publication:
- December 1959
-
- Article
- Export citation
Covering space with equal spheres
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-157
- Print publication:
- December 1959
-
- Article
- Export citation
On the enumerative geometry of triangles
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-164
- Print publication:
- December 1959
-
- Article
- Export citation
Rational polygons
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, p. 98
- Print publication:
- December 1959
-
- Article
- Export citation
Note on the motion of fluid in a curved pipe
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-85
- Print publication:
- June 1959
-
- Article
-
- You have access
- Export citation
MTK volume 6 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1959
-
- Article
-
- You have access
- Export citation
Lattice coverings of space
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-39
- Print publication:
- June 1959
-
- Article
- Export citation
The stability of a column of rotating liquid
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-32
- Print publication:
- June 1959
-
- Article
- Export citation
The genus field and genus group in finite number fields
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-46
- Print publication:
- June 1959
-
- Article
- Export citation
Simple rings without zero-divisors, and Lie division rings
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-18
- Print publication:
- June 1959
-
- Article
- Export citation
Combinatorial extreme value distributions
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-76
- Print publication:
- June 1959
-
- Article
- Export citation
Products on spheres
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1959
-
- Article
- Export citation
Elastic equilibrium of completely aeolotropic cylinders: extension by longitudinal lateral loading and end forces
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-62
- Print publication:
- June 1959
-
- Article
- Export citation
A generalization of Ascoli's theorem
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-24
- Print publication:
- June 1959
-
- Article
- Export citation
Indefinite quadratic forms
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
- Print publication:
- December 1958
-
- Article
- Export citation
A disproof of a conjecture of Pólya
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-145
- Print publication:
- December 1958
-
- Article
- Export citation
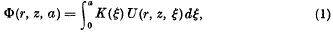
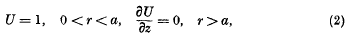
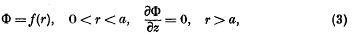
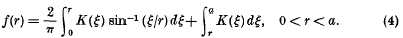
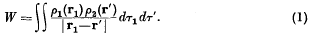
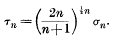
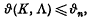

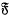
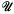 .
.