Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
The addition of norm forms
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-82
- Print publication:
- June 1962
-
- Article
- Export citation
On some axisymmetrical two sphere potential problems
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-70
- Print publication:
- June 1962
-
- Article
- Export citation
An extension of a theorem of König on graphs
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 9-10
- Print publication:
- June 1962
-
- Article
- Export citation
Continued fractions of transcendental numbers
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-8
- Print publication:
- June 1962
-
- Article
- Export citation
MTK volume 9 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. f1
- Print publication:
- June 1962
-
- Article
-
- You have access
- Export citation
Some axially symmetric stress distributions in elastic solids containing penny-shaped cracks. II. Cracks in solids under torsion
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-37
- Print publication:
- June 1962
-
- Article
- Export citation
A slow fluid motion between two spheres
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-87
- Print publication:
- June 1962
-
- Article
- Export citation
Some Abelian results for Dirichlet series
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-53
- Print publication:
- June 1962
-
- Article
- Export citation
The group of rotations in a plane over GF(2n)
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-74
- Print publication:
- June 1962
-
- Article
- Export citation
MTK volume 8 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1961
-
- Article
-
- You have access
- Export citation
The stability of a plane Alfvén wave of finite amplitude
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-141
- Print publication:
- December 1961
-
- Article
- Export citation
On Steiner's network problem
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-132
- Print publication:
- December 1961
-
- Article
- Export citation
Note on a biharmonic Green's function
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-169
- Print publication:
- December 1961
-
- Article
- Export citation
Index to Volume 8
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, p. 173
- Print publication:
- December 1961
-
- Article
- Export citation
Strong cylindrical shock waves in magnetogasdynamics
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-120
- Print publication:
- December 1961
-
- Article
- Export citation
Polynomials over finite fields with minimal value sets
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 121-130
- Print publication:
- December 1961
-
- Article
- Export citation
Discriminants and module invariants over a Dedekind domain
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-172
- Print publication:
- December 1961
-
- Article
- Export citation
The quadric threefold cone of S4
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-98
- Print publication:
- December 1961
-
- Article
- Export citation
Primitive distributively generated near-rings
-
- Journal:
- Mathematika / Volume 8 / Issue 2 / December 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-158
- Print publication:
- December 1961
-
- Article
- Export citation
On the non-specialisation of intersections on a singular variety
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-44
- Print publication:
- June 1961
-
- Article
- Export citation
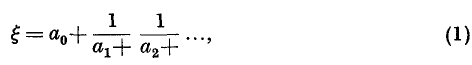

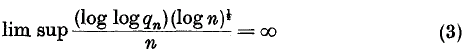
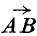 .
.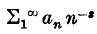 and if
and if 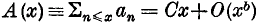 where 0 ≤
where 0 ≤