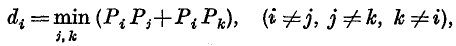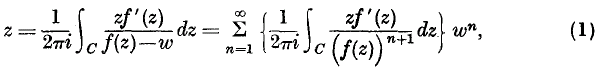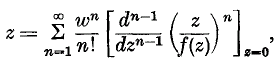Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Plane elastostatic boundary value problems (I). Stresses in an elliptic plate
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-28
- Print publication:
- June 1963
-
- Article
- Export citation
A problematic identity
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-12
- Print publication:
- June 1963
-
- Article
- Export citation
Note on the basic assumptions of elastic plate theories
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
- Print publication:
- December 1962
-
- Article
- Export citation
Monoidal transformations in a one-dimensional local ring
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-144
- Print publication:
- December 1962
-
- Article
- Export citation
MTK volume 9 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. f1
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
Sets non-σ-finite for Hausdorff measures
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 95-103
- Print publication:
- December 1962
-
- Article
- Export citation
On circuits and subgraphs of chromatic graphs
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-175
- Print publication:
- December 1962
-
- Article
- Export citation
Index to volume 9
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. 176
- Print publication:
- December 1962
-
- Article
- Export citation
Approximation properties of measures generated by continuous set functions
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-156
- Print publication:
- December 1962
-
- Article
- Export citation
A result relating to the local uniformisation theorem
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-110
- Print publication:
- December 1962
-
- Article
- Export citation
The stability of an incompressible jet with an aligned magnetic field
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-169
- Print publication:
- December 1962
-
- Article
- Export citation
On the genus of curves over finite fields
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-117
- Print publication:
- December 1962
-
- Article
- Export citation
On non-ramified extensions with prescribed Galois group
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-134
- Print publication:
- December 1962
-
- Article
- Export citation
A transcendence measure for E-functions
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-161
- Print publication:
- December 1962
-
- Article
- Export citation
A note on the Hilbert functions of certain ideals which are defined by matrices
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-126
- Print publication:
- December 1962
-
- Article
- Export citation
Average distances between points in a square
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-114
- Print publication:
- December 1962
-
- Article
- Export citation
Reversion of a formal power series
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-94
- Print publication:
- June 1962
-
- Article
- Export citation
Thermal damping of a vibrating elastic body
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-48
- Print publication:
- June 1962
-
- Article
- Export citation
A moment theory of elastic plates
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 11-24
- Print publication:
- June 1962
-
- Article
- Export citation
Two special cubic surfaces
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-56
- Print publication:
- June 1962
-
- Article
- Export citation
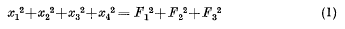
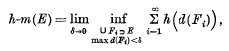
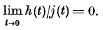
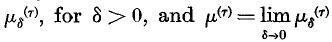 (see §3). When, for every
(see §3). When, for every 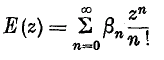
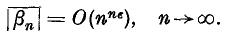
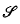 of
of