Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Coprime mappings between sets of consecutive integers
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-136
- Print publication:
- December 1963
-
- Article
- Export citation
Decomposable convex polyhedra
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-95
- Print publication:
- December 1963
-
- Article
- Export citation
Index to volume 10
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, p. 165
- Print publication:
- December 1963
-
- Article
- Export citation
A note on cracks under longitudinal shear
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-113
- Print publication:
- December 1963
-
- Article
- Export citation
Index to Volume 1–10 1954–1963
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-182
- Print publication:
- December 1963
-
- Article
- Export citation
A Stokes flow problem between two non-concentric cylinders
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-156
- Print publication:
- December 1963
-
- Article
- Export citation
Covering a sphere with spheres
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-164
- Print publication:
- December 1963
-
- Article
- Export citation
Algebraic integral representations by arbitrary forms
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-100
- Print publication:
- December 1963
-
- Article
- Export citation
Rational polygons
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
- Print publication:
- December 1963
-
- Article
- Export citation
On the embedding of complete graphs in orientable surfaces
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-83
- Print publication:
- June 1963
-
- Article
- Export citation
A slow motion of viscous liquid caused by the rotation of a solid sphere
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-24
- Print publication:
- June 1963
-
- Article
- Export citation
On a selection problem for a sequence of finite sets
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-63
- Print publication:
- June 1963
-
- Article
- Export citation
A note on the axisymmetric Stokes flow of viscous fluid past a spherical cap
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-78
- Print publication:
- June 1963
-
- Article
- Export citation
Multiple packing of spherical caps
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 84-88
- Print publication:
- June 1963
-
- Article
- Export citation
Plane elastostatic boundary value problems (II). The role of inversion
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-34
- Print publication:
- June 1963
-
- Article
- Export citation
Approximation of convex surfaces by algebraic surfaces
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-71
- Print publication:
- June 1963
-
- Article
- Export citation
The Hilbert function of the tensor product of two multigraded modules
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-57
- Print publication:
- June 1963
-
- Article
- Export citation
Plane elastostatic boundary value problems (III). Stresses in a parabolic mound
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-42
- Print publication:
- June 1963
-
- Article
- Export citation
MTK volume 10 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1963
-
- Article
-
- You have access
- Export citation
The Hausdorff measure of the intersection of sets of positive Lebesgue measure
-
- Journal:
- Mathematika / Volume 10 / Issue 1 / June 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1963
-
- Article
- Export citation
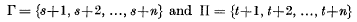
 be a set of points on a sphere, centre
be a set of points on a sphere, centre  . Let
. Let  provides a
provides a 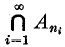 contains a perfect subset (and is therefore of power
contains a perfect subset (and is therefore of power 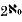 ). They asked for what Hausdorff measure functions
). They asked for what Hausdorff measure functions 