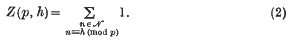Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
An investigation of the elastic strip and the annulus
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-200
- Print publication:
- December 1965
-
- Article
- Export citation
A minimal density plane covering problem
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 226-234
- Print publication:
- December 1965
-
- Article
- Export citation
Convection in a self-gravitating fluid sphere
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-137
- Print publication:
- December 1965
-
- Article
- Export citation
Index to volume 12
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, p. 257
- Print publication:
- December 1965
-
- Article
- Export citation
Biquadratic congruences
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-160
- Print publication:
- December 1965
-
- Article
- Export citation
The distribution of solutions of congruences
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 176-192
- Print publication:
- December 1965
-
- Article
- Export citation
On the large sieve
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
- Print publication:
- December 1965
-
- Article
- Export citation
Surface waves over a submerged circular cylinder
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 235-245
- Print publication:
- December 1965
-
- Article
- Export citation
On linear relations between roots of unity
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-117
- Print publication:
- December 1965
-
- Article
- Export citation
On the dimension of a graph
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-122
- Print publication:
- December 1965
-
- Article
- Export citation
Lattice coverings of five space by spheres
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-150
- Print publication:
- December 1965
-
- Article
- Export citation
Metric simultaneous diophantine approximation (II)
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-127
- Print publication:
- December 1965
-
- Article
- Export citation
MTK volume 12 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1965
-
- Article
-
- You have access
- Export citation
Oscillatory motion of an elastico-viscous liquid contained between two coaxial cylinders
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 246-256
- Print publication:
- December 1965
-
- Article
- Export citation
Oscillating viscous flows
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-175
- Print publication:
- December 1965
-
- Article
- Export citation
Diffusion from an elevated point source into a turbulent atmosphere
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
- Print publication:
- June 1965
-
- Article
- Export citation
A note on linear transversely isotropic fluids
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 27-29
- Print publication:
- June 1965
-
- Article
- Export citation
Cubic Diophantine equations: the necessary congruence condition
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
- Print publication:
- June 1965
-
- Article
- Export citation
Scalar matrix quadratic residues
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-96
- Print publication:
- June 1965
-
- Article
- Export citation
On the large sieves of Linnik and Rényi
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1965
-
- Article
- Export citation
 . The problem is to find the exact lower bound of the lower density for any saturated set of circles. We show that it is φ/(6√3) provided the circles are disjoint. The general case, when they may overlap, remains unsolved.
. The problem is to find the exact lower bound of the lower density for any saturated set of circles. We show that it is φ/(6√3) provided the circles are disjoint. The general case, when they may overlap, remains unsolved.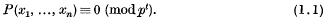
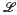
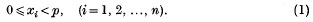
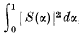 where
where 
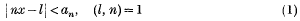
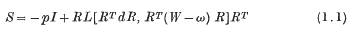
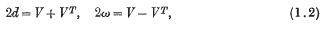
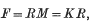
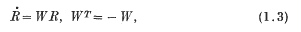
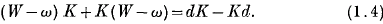
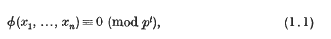


 be a non-empty subset of the set of integers
be a non-empty subset of the set of integers