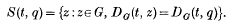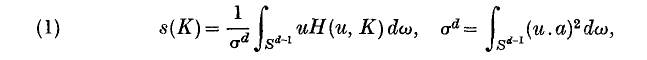Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Approximations by polytopes with projectively regular facets
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-195
- Print publication:
- December 1966
-
- Article
- Export citation
An inequality for sequence transformations
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 26-41
- Print publication:
- June 1966
-
- Article
- Export citation
Reducible convex sets
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-50
- Print publication:
- June 1966
-
- Article
- Export citation
Laguerre functions with truncated domain
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-56
- Print publication:
- June 1966
-
- Article
- Export citation
Permutation mappings in finite projective planes
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-48
- Print publication:
- June 1966
-
- Article
- Export citation
Plane parallel flow of a dusty gas
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-109
- Print publication:
- June 1966
-
- Article
- Export citation
A differential equation in fluid mechanics
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-53
- Print publication:
- June 1966
-
- Article
- Export citation
On the reversed flow solutions of the Falkner-Skan equation
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1966
-
- Article
- Export citation
Mappings of finite sets
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-25
- Print publication:
- June 1966
-
- Article
- Export citation
On the construction of measures
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-68
- Print publication:
- June 1966
-
- Article
- Export citation
On the exponent of convergence of a packing of spheres
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-59
- Print publication:
- June 1966
-
- Article
- Export citation
Oscillatory motion of an elastico-viscous liquid contained between two concentric spheres
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-89
- Print publication:
- June 1966
-
- Article
- Export citation
Biquadratic congruences: an acknowledgement
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, p. 90
- Print publication:
- June 1966
-
- Article
- Export citation
MTK volume 13 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1966
-
- Article
-
- You have access
- Export citation
The Carathéodory limiting spherical shells in the euclidean hypersphere
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-75
- Print publication:
- June 1966
-
- Article
- Export citation
Short proof of Menger's graph theorem
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-44
- Print publication:
- June 1966
-
- Article
- Export citation
The values of a trigonometrical polynomial at well spaced points
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-96
- Print publication:
- June 1966
-
- Article
- Export citation
A valuation property of Steiner points
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-82
- Print publication:
- June 1966
-
- Article
- Export citation
Valuation rings formed by ascending sequences of quotient rings
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-22
- Print publication:
- June 1966
-
- Article
- Export citation
The densest double lattice packing of four-spheres
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-142
- Print publication:
- December 1965
-
- Article
- Export citation
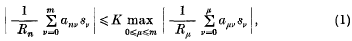
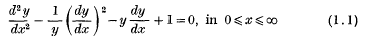
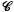 of subsets of
of subsets of 
 is packed into the open unit
is packed into the open unit 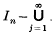 has zero volume. Then, of course,
has zero volume. Then, of course, 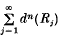 is convergent and it can be shown, for
is convergent and it can be shown, for 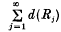 is divergent. Let the exponent of convergence of the packing
is divergent. Let the exponent of convergence of the packing 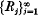 of those real numbers
of those real numbers 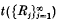 is divergent and let
is divergent and let