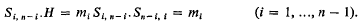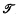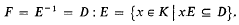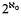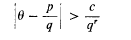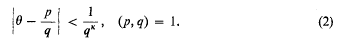Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
Index to volume 15
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 228
- Print publication:
- December 1968
-
- Article
- Export citation
Diagrams for centrally symmetric polytopes
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-138
- Print publication:
- December 1968
-
- Article
- Export citation
On the group of automorphisms of the Euclidean hypersphere
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-198
- Print publication:
- December 1968
-
- Article
- Export citation
Specialization of Cremona transformations
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-177
- Print publication:
- December 1968
-
- Article
- Export citation
On Hausdorff dimension of projections
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-155
- Print publication:
- December 1968
-
- Article
- Export citation
Irrotational gravity waves of finite height: a numerical study
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-148
- Print publication:
- December 1968
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (IV)
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 204-216
- Print publication:
- December 1968
-
- Article
- Export citation
Corrigendum: Mathematika Volume 14, 1967
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 227
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
MTK volume 15 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
On nodes of degree two in random trees
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-192
- Print publication:
- December 1968
-
- Article
- Export citation
Integral domains in which each non-zero ideal is divisorial
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-170
- Print publication:
- December 1968
-
- Article
- Export citation
Asymptotic expansions in certain second order nonhomogeneous differential equations
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
- Print publication:
- June 1968
-
- Article
- Export citation
On acyclic simplicial complexes
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-122
- Print publication:
- June 1968
-
- Article
- Export citation
A theorem on the existence of non-σ-finite subsets
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-62
- Print publication:
- June 1968
-
- Article
- Export citation
On the distribution of Fekete points
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 70-75
- Print publication:
- June 1968
-
- Article
- Export citation
On a two-dimensional exterior Stokes flow with mixed boundary conditions
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-114
- Print publication:
- June 1968
-
- Article
- Export citation
The average of the least primitive root
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-50
- Print publication:
- June 1968
-
- Article
- Export citation
On an integral equation
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 22-29
- Print publication:
- June 1968
-
- Article
- Export citation
Christoffel's problem for general convex bodies
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-21
- Print publication:
- June 1968
-
- Article
- Export citation
A note on Thue's theorem
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-87
- Print publication:
- June 1968
-
- Article
- Export citation
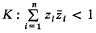 be the unit hypersphere. Further, let
be the unit hypersphere. Further, let 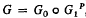 , where
, where 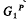 is a 2
is a 2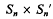 of two
of two 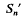 (regarded as an irreducible algebraic system of ∞
(regarded as an irreducible algebraic system of ∞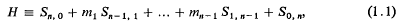
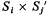 of
of