Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Sums and products of functions in the MacLane class A
-
- Journal:
- Mathematika / Volume 16 / Issue 1 / June 1969
- Published online by Cambridge University Press:
- 26 February 2010, pp. 86-87
- Print publication:
- June 1969
-
- Article
- Export citation
Selberg's sieve with weights
-
- Journal:
- Mathematika / Volume 16 / Issue 1 / June 1969
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-22
- Print publication:
- June 1969
-
- Article
- Export citation
On partitioning ordered sets into cofinal subsets
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 217-222
- Print publication:
- December 1968
-
- Article
- Export citation
The large sieve inequality for algebraic number fields
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-187
- Print publication:
- December 1968
-
- Article
- Export citation
Decomposition of functions whose partial derivatives are measures
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-152
- Print publication:
- December 1968
-
- Article
- Export citation
Some applications of a theorem of Rado
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-203
- Print publication:
- December 1968
-
- Article
- Export citation
Artin's conjecture on the average
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-226
- Print publication:
- December 1968
-
- Article
- Export citation
A presentation of SL2 for Euclidean imaginary quadratic number fields
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-163
- Print publication:
- December 1968
-
- Article
- Export citation
Index to volume 15
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 228
- Print publication:
- December 1968
-
- Article
- Export citation
Diagrams for centrally symmetric polytopes
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-138
- Print publication:
- December 1968
-
- Article
- Export citation
On the group of automorphisms of the Euclidean hypersphere
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-198
- Print publication:
- December 1968
-
- Article
- Export citation
Specialization of Cremona transformations
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-177
- Print publication:
- December 1968
-
- Article
- Export citation
On Hausdorff dimension of projections
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-155
- Print publication:
- December 1968
-
- Article
- Export citation
Irrotational gravity waves of finite height: a numerical study
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-148
- Print publication:
- December 1968
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (IV)
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 204-216
- Print publication:
- December 1968
-
- Article
- Export citation
Corrigendum: Mathematika Volume 14, 1967
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, p. 227
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
MTK volume 15 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1968
-
- Article
-
- You have access
- Export citation
On nodes of degree two in random trees
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-192
- Print publication:
- December 1968
-
- Article
- Export citation
Integral domains in which each non-zero ideal is divisorial
-
- Journal:
- Mathematika / Volume 15 / Issue 2 / December 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-170
- Print publication:
- December 1968
-
- Article
- Export citation
Asymptotic expansions in certain second order nonhomogeneous differential equations
-
- Journal:
- Mathematika / Volume 15 / Issue 1 / June 1968
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
- Print publication:
- June 1968
-
- Article
- Export citation
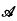 be the class of non-constant functions
be the class of non-constant functions 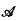 be a (finite) non-empty sequence of integers, and let
be a (finite) non-empty sequence of integers, and let 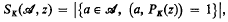
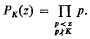
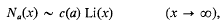
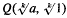 .
.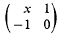 as
as 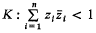 be the unit hypersphere. Further, let
be the unit hypersphere. Further, let 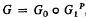 , where
, where 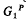 is a 2
is a 2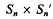 of two
of two 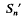 (regarded as an irreducible algebraic system of ∞
(regarded as an irreducible algebraic system of ∞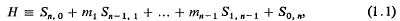
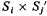 of
of