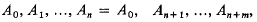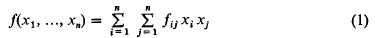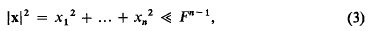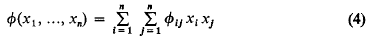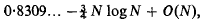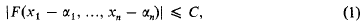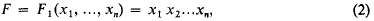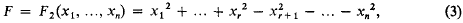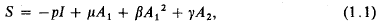Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
Symmetrical sets of constant width and their partitions
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-111
- Print publication:
- June 1971
-
- Article
- Export citation
On a problem of Gauthier
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 126-129
- Print publication:
- June 1971
-
- Article
- Export citation
On the representation of positive integers as sums of three cubes of positive rational numbers
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-99
- Print publication:
- June 1971
-
- Article
- Export citation
Fractional powers of a submodule of an algebra
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 8-13
- Print publication:
- June 1971
-
- Article
- Export citation
On the minimum points of a positive quadratic form
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
- Print publication:
- June 1971
-
- Article
- Export citation
On plane coverings with convex domains
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
- Print publication:
- June 1971
-
- Article
- Export citation
The existence and uniqueness of a similarity solution of boundary-layer theory
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-19
- Print publication:
- June 1971
-
- Article
- Export citation
Homogeneous quadratic equations
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-4
- Print publication:
- June 1971
-
- Article
- Export citation
The lengths of limbs of random trees
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-81
- Print publication:
- June 1971
-
- Article
- Export citation
Short surface waves due to an oscillating half-immersed sphere
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-39
- Print publication:
- June 1971
-
- Article
- Export citation
Some embeddings of Lie groups in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 152-156
- Print publication:
- June 1971
-
- Article
- Export citation
On pseudo-polynomials
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-77
- Print publication:
- June 1971
-
- Article
- Export citation
A determinant of linear forms
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 100-104
- Print publication:
- June 1971
-
- Article
- Export citation
A compact set of disjoint line segments in E3 whose end set has positive measure
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 112-125
- Print publication:
- June 1971
-
- Article
- Export citation
A note on the steady longitudinal motion of an insulating cylinder in a conducting fluid
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 130-133
- Print publication:
- June 1971
-
- Article
- Export citation
A convex body with a false centre is an ellipsoid
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-59
- Print publication:
- June 1971
-
- Article
- Export citation
When is a linear viscoelastic material elastic?
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-137
- Print publication:
- June 1971
-
- Article
- Export citation
MTK volume 18 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1971
-
- Article
-
- You have access
- Export citation
On uniqueness of flows for a class of second-order fluids
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 333-337
- Print publication:
- December 1970
-
- Article
- Export citation
The distribution of rational points on hypersurfaces defined over a finite field
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 328-332
- Print publication:
- December 1970
-
- Article
- Export citation

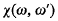 is called the distance between ω and ω′ in the spherical or in the chordal metric.
is called the distance between ω and ω′ in the spherical or in the chordal metric.