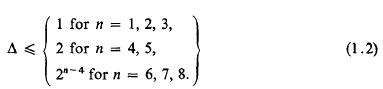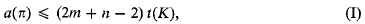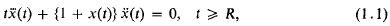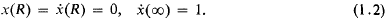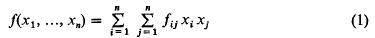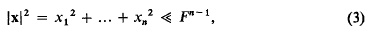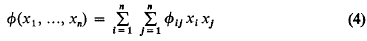Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Index to volume 18
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 291-292
- Print publication:
- December 1971
-
- Article
- Export citation
Note on a theorem of Weil-Abels
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-187
- Print publication:
- December 1971
-
- Article
- Export citation
On the smoothing of stochastic couples in the theory of Brownian rotations of slender particles
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-254
- Print publication:
- December 1971
-
- Article
- Export citation
Properties and characterizations of k-trees
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-151
- Print publication:
- June 1971
-
- Article
- Export citation
On the distribution of Fekete points II
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-49
- Print publication:
- June 1971
-
- Article
- Export citation
Trees with Hamiltonian square
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-140
- Print publication:
- June 1971
-
- Article
- Export citation
An extension of stone's partitioning theorem for ordered sets
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 5-7
- Print publication:
- June 1971
-
- Article
- Export citation
Toroidal maps with prescribed types of vertices and faces
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-90
- Print publication:
- June 1971
-
- Article
- Export citation
Symmetrical sets of constant width and their partitions
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-111
- Print publication:
- June 1971
-
- Article
- Export citation
On a problem of Gauthier
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 126-129
- Print publication:
- June 1971
-
- Article
- Export citation
On the representation of positive integers as sums of three cubes of positive rational numbers
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-99
- Print publication:
- June 1971
-
- Article
- Export citation
Fractional powers of a submodule of an algebra
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 8-13
- Print publication:
- June 1971
-
- Article
- Export citation
On the minimum points of a positive quadratic form
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
- Print publication:
- June 1971
-
- Article
- Export citation
On plane coverings with convex domains
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
- Print publication:
- June 1971
-
- Article
- Export citation
The existence and uniqueness of a similarity solution of boundary-layer theory
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-19
- Print publication:
- June 1971
-
- Article
- Export citation
Homogeneous quadratic equations
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-4
- Print publication:
- June 1971
-
- Article
- Export citation
The lengths of limbs of random trees
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-81
- Print publication:
- June 1971
-
- Article
- Export citation
Short surface waves due to an oscillating half-immersed sphere
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-39
- Print publication:
- June 1971
-
- Article
- Export citation
Some embeddings of Lie groups in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 152-156
- Print publication:
- June 1971
-
- Article
- Export citation
On pseudo-polynomials
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-77
- Print publication:
- June 1971
-
- Article
- Export citation
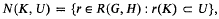
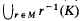 is a relatively compact subset of
is a relatively compact subset of 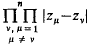
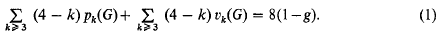

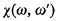 is called the distance between ω and ω′ in the spherical or in the chordal metric.
is called the distance between ω and ω′ in the spherical or in the chordal metric.