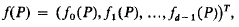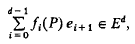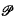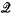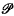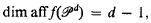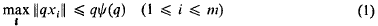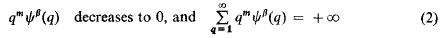Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
On converging solid spheres in a highly viscous fluid
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 250-254
- Print publication:
- December 1970
-
- Article
- Export citation
Index to volume 17
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, p. 338
- Print publication:
- December 1970
-
- Article
- Export citation
Reuleaux polytopes
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 315-323
- Print publication:
- December 1970
-
- Article
- Export citation
Some dimensional properties of generalised difference sets
-
- Journal:
- Mathematika / Volume 17 / Issue 2 / December 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-188
- Print publication:
- December 1970
-
- Article
- Export citation
Singular integral equations with logarithmic kernels
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-56
- Print publication:
- June 1970
-
- Article
- Export citation
Corrigendum and addendum: an analogue of a problem of Littlewood
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-178
- Print publication:
- June 1970
-
- Article
- Export citation
The number of d-polytopes with d+3 vertices
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-132
- Print publication:
- June 1970
-
- Article
- Export citation
Solution of some boundary value problems in potential theory
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-101
- Print publication:
- June 1970
-
- Article
- Export citation
The critical layer in stratified shear flow
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-119
- Print publication:
- June 1970
-
- Article
- Export citation
Measure function properties of the asymmetric Cauchy process
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-78
- Print publication:
- June 1970
-
- Article
- Export citation
Convex bodies of constant outer p-measure
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-27
- Print publication:
- June 1970
-
- Article
- Export citation
A local form of the Phragmén-lindelöf indicator
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-172
- Print publication:
- June 1970
-
- Article
- Export citation
A note on the classgroup of integral group rings of some cyclic groups
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-81
- Print publication:
- June 1970
-
- Article
- Export citation
Asymptotic formulas for the number of self-complementary graphs and digraphs
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-90
- Print publication:
- June 1970
-
- Article
- Export citation
The symmetric elements of a semi-simple S-ring
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-84
- Print publication:
- June 1970
-
- Article
- Export citation
A linear set of infinite measure with no two points having integral ratio
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-138
- Print publication:
- June 1970
-
- Article
- Export citation
Dense sequences of convex polytopes
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 28-38
- Print publication:
- June 1970
-
- Article
- Export citation
Probability, Hausdorff dimension, and fractional distribution
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-67
- Print publication:
- June 1970
-
- Article
- Export citation
MTK volume 17 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1970
-
- Article
-
- You have access
- Export citation
The directions of the line segments and of the r-dimensional balls on the boundary of a convex body in Euclidean space
-
- Journal:
- Mathematika / Volume 17 / Issue 1 / June 1970
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-20
- Print publication:
- June 1970
-
- Article
- Export citation
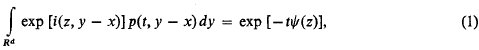
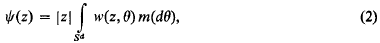
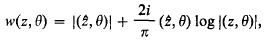
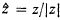 . It follows that for each
. It follows that for each 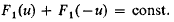

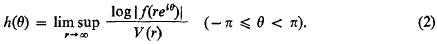
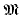 ), Γ a finite abelian group,
), Γ a finite abelian group, 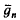 of self-complementary graphs and the number
of self-complementary graphs and the number 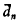 of self-complementary digraphs were expressed by Read [4] in terms of cycle indexes of the appropriate pair groups. These formulas for
of self-complementary digraphs were expressed by Read [4] in terms of cycle indexes of the appropriate pair groups. These formulas for 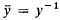 for
for 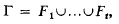
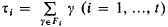 of
of 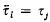 .
.