Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
On the classgroup of integral grouprings of finite Abelian groups II
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-56
- Print publication:
- June 1972
-
- Article
- Export citation
Class groups for integral representations of metacyclic groups
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-111
- Print publication:
- June 1972
-
- Article
- Export citation
On the uniqueness of solutions of the Falkner-Skan equation
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-133
- Print publication:
- June 1972
-
- Article
- Export citation
A generalized lower-bound conjecture for simplicial polytopes
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-273
- Print publication:
- December 1971
-
- Article
- Export citation
Sets which are null or non-sigma-finite for every translation invariant measure
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-162
- Print publication:
- December 1971
-
- Article
- Export citation
A note on a problem of Gauthier
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-275
- Print publication:
- December 1971
-
- Article
- Export citation
MTK volume 18 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1971
-
- Article
-
- You have access
- Export citation
On almost discrete spaces
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 163-167
- Print publication:
- December 1971
-
- Article
- Export citation
On the large sieve method in GF (q, x)
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-184
- Print publication:
- December 1971
-
- Article
- Export citation
Polyhedral diagrams for sections of the non-negative orthant
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 255-263
- Print publication:
- December 1971
-
- Article
- Export citation
Integral representations of solutions to a class of fourth order elliptic equations in three independent variables
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 283-290
- Print publication:
- December 1971
-
- Article
- Export citation
A note on boundedly countably paracompact spaces
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 168-171
- Print publication:
- December 1971
-
- Article
- Export citation
On the non-linear response of a marginally unstable plane parallel flow to a three-dimensional disturbance
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 219-239
- Print publication:
- December 1971
-
- Article
- Export citation
Stable linear maps
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 276-282
- Print publication:
- December 1971
-
- Article
- Export citation
Three distribution identities and Maxwell's atomic field equations including the Röntgen current
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 240-246
- Print publication:
- December 1971
-
- Article
- Export citation
Properties of finite character of independence spaces
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-208
- Print publication:
- December 1971
-
- Article
- Export citation
Measures not approximable or not specifiable by means of balls
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-160
- Print publication:
- December 1971
-
- Article
- Export citation
Chern classes and metacyclic p-groups
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 196-200
- Print publication:
- December 1971
-
- Article
- Export citation
A sequence of multiple points on an algebraic variety which gives rise to a valuation ring
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-218
- Print publication:
- December 1971
-
- Article
- Export citation
Wing-body interaction in supersonic flow past dihedral wings
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-195
- Print publication:
- December 1971
-
- Article
- Export citation
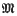 ) of the maximal order
) of the maximal order 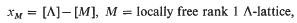
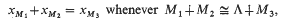
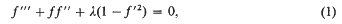
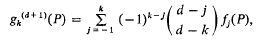

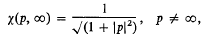
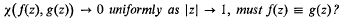 Clunie [4] has answered this problem in the negative by constructing different meromorphic functions
Clunie [4] has answered this problem in the negative by constructing different meromorphic functions