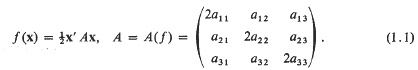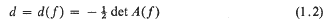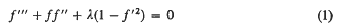Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Fredholm formulae and the Riesz-theory—a base for the null space of I— λoK
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-220
- Print publication:
- December 1972
-
- Article
- Export citation
A Hamiltonian theory for weakly interacting vortices
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 169-179
- Print publication:
- December 1972
-
- Article
- Export citation
MTK volume 19 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1972
-
- Article
-
- You have access
- Export citation
Asymmetric sets of residues
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-199
- Print publication:
- December 1972
-
- Article
- Export citation
Axisymmetric inertial oscillations of a fluid in a rotating spherical shell
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 163-168
- Print publication:
- December 1972
-
- Article
- Export citation
On some solutions of the Falkner-Skan equation
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-83
- Print publication:
- June 1972
-
- Article
- Export citation
The distribution of polynomial sequences
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-50
- Print publication:
- June 1972
-
- Article
- Export citation
On the exponential sum
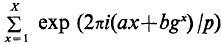
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 84-87
- Print publication:
- June 1972
-
- Article
- Export citation
A note on primitive roots in finite fields
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 112-114
- Print publication:
- June 1972
-
- Article
- Export citation
Measures of Hausdorff-type, and Brownian motion
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-119
- Print publication:
- June 1972
-
- Article
- Export citation
MTK volume 19 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1972
-
- Article
-
- You have access
- Export citation
A note on linear thermoelasticity
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-75
- Print publication:
- June 1972
-
- Article
- Export citation
The realization of distances within sets in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-24
- Print publication:
- June 1972
-
- Article
- Export citation
The zeros of trigonometrical polynomials
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-90
- Print publication:
- June 1972
-
- Article
- Export citation
A note on the locally finite sum theorem
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 121-127
- Print publication:
- June 1972
-
- Article
- Export citation
On the fractional parts of a set of points
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-68
- Print publication:
- June 1972
-
- Article
- Export citation
Simple one-point extensions of tournaments
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-62
- Print publication:
- June 1972
-
- Article
- Export citation
One-class genera of positive ternary quadratic forms
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-104
- Print publication:
- June 1972
-
- Article
- Export citation
Reverse flow solutions of the Falkner-Skan equation for λ > 1
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-138
- Print publication:
- June 1972
-
- Article
- Export citation
Some problems on consecutive prime numbers
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-95
- Print publication:
- June 1972
-
- Article
- Export citation
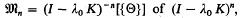 and in particular for the null space
and in particular for the null space 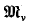 of
of 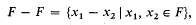
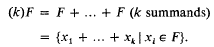
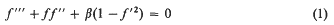
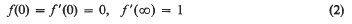
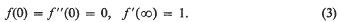
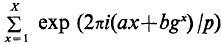
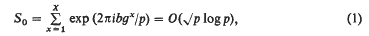
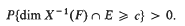
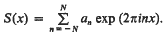
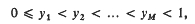
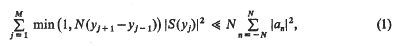
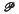 be a topological property. We say that the locally finite sum theorem holds for the property
be a topological property. We say that the locally finite sum theorem holds for the property 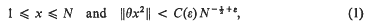
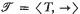 is a relational structure on the non-empty set
is a relational structure on the non-empty set 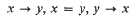
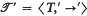 is a
is a 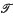 , and
, and 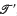 , if
, if