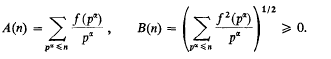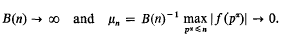Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
References
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 191-201
-
- Chapter
- Export citation
15 - Automorphisms of graphs
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 115-121
-
- Chapter
- Export citation
19 - The covering-graph construction
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 149-154
-
- Chapter
- Export citation
21 - Feasibility of intersection arrays
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 164-172
-
- Chapter
- Export citation
3 - Regular graphs and line graphs
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 14-22
-
- Chapter
- Export citation
Preface
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp vii-viii
-
- Chapter
- Export citation
Index
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 202-205
-
- Chapter
- Export citation
6 - The tree-number
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 38-43
-
- Chapter
- Export citation
8 - Vertex-partitions and the spectrum
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 52-60
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 1-4
-
- Chapter
- Export citation
10 - Subgraph expansions
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 73-80
-
- Chapter
- Export citation
17 - Symmetric graphs
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 130-137
-
- Chapter
- Export citation
22 - Imprimitivity
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 173-179
-
- Chapter
- Export citation
Contents
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp v-vi
-
- Chapter
- Export citation
2 - The spectrum of a graph
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 7-13
-
- Chapter
- Export citation
14 - Chromatic polynomials and spanning trees
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 106-112
-
- Chapter
- Export citation
The residual set dimension of the Apollonian packing
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-174
- Print publication:
- December 1973
-
- Article
- Export citation
On the slow viscous rotation of a body straddling the interface between two immiscible semi-infinite fluids
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-196
- Print publication:
- December 1973
-
- Article
- Export citation
Two singular measures can agree on balls
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 224-225
- Print publication:
- December 1973
-
- Article
- Export citation
A class of additive arithmetic functions with asymptotically normal distribution
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-154
- Print publication:
- December 1973
-
- Article
- Export citation