Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Outerthickness and outercoarseness of graphs
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 57-60
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp v-vi
-
- Chapter
- Export citation
A note on embedding latin rectangles
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 69-74
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp i-ii
-
- Chapter
- Export citation
Shapes of worn stones
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
- Print publication:
- June 1974
-
- Article
- Export citation
The class groups of quaternion and dihedral 2-groups
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-71
- Print publication:
- June 1974
-
- Article
- Export citation
On irregularities of integer sequences
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-106
- Print publication:
- June 1974
-
- Article
- Export citation
The number of neighbourly d-polytopes with d+3 vertices
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 26-31
- Print publication:
- June 1974
-
- Article
- Export citation
The zeros of a function occurring in the solution of the Graetz problem
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-63
- Print publication:
- June 1974
-
- Article
- Export citation
The average size of gaps between primes
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-100
- Print publication:
- June 1974
-
- Article
- Export citation
Class groups of metacyclic groups of order p'q,p a regular prime
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-95
- Print publication:
- June 1974
-
- Article
- Export citation
Primitive Radon partitions
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-37
- Print publication:
- June 1974
-
- Article
- Export citation
The stability of an expanding circular vortex sheet
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-133
- Print publication:
- June 1974
-
- Article
- Export citation
On isolated fixed points of group actions on poincaré complexes
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 114-115
- Print publication:
- June 1974
-
- Article
- Export citation
On the structure of instability bursts in three-dimensional parallel flow
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-146
- Print publication:
- June 1974
-
- Article
- Export citation
Note on difference-covers that are not k-sum-covers
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-109
- Print publication:
- June 1974
-
- Article
- Export citation
The 3-class groups of non-Galois cubic fields—I
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-89
- Print publication:
- June 1974
-
- Article
- Export citation
MTK volume 21 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1974
-
- Article
-
- You have access
- Export citation
Decomposition of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-25
- Print publication:
- June 1974
-
- Article
- Export citation
Families of compact sets and their universals
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-127
- Print publication:
- June 1974
-
- Article
- Export citation
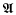 be a = ℤ-order in
be a = ℤ-order in 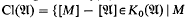 locally isomorphic to
locally isomorphic to 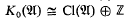 as all ℤΓ projectives are locally free [12].)
as all ℤΓ projectives are locally free [12].)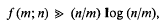
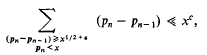
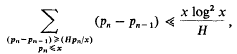
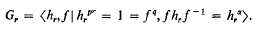
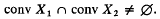
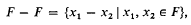
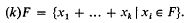
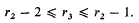
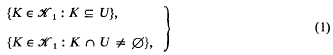
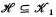 we shall be concerned with sets in [0, 1] ×
we shall be concerned with sets in [0, 1] ×