Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Primitive polynomial subsequences
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-247
- Print publication:
- December 1974
-
- Article
- Export citation
The integral closure need not be a Prüfer domain
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-238
- Print publication:
- December 1974
-
- Article
- Export citation
The inverse Stefan problem for the heat equation in two space variables
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 282-286
- Print publication:
- December 1974
-
- Article
- Export citation
A lower bound for the L1 norm of exponential sums
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-159
- Print publication:
- December 1974
-
- Article
- Export citation
A note on the false centre problem
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-227
- Print publication:
- December 1974
-
- Article
- Export citation
A decision procedure using the geometry of convex sets
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-206
- Print publication:
- December 1974
-
- Article
- Export citation
Index to volume 21
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, p. 287
- Print publication:
- December 1974
-
- Article
- Export citation
The convex generation of convex Borel sets in locally convex spaces
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-215
- Print publication:
- December 1974
-
- Article
- Export citation
Subsets of positive finite measure in the space of compact subsets of the unit interval
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-192
- Print publication:
- December 1974
-
- Article
- Export citation
Kinematic measures for sets of support figures
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-281
- Print publication:
- December 1974
-
- Article
- Export citation
MTK volume 21 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1974
-
- Article
-
- You have access
- Export citation
Generalisation of Fisher's inequality to fields with more than one element
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 9-14
-
- Chapter
- Export citation
Contents
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp iii-iv
-
- Chapter
- Export citation
The distance between nodes in recursive trees
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 125-132
-
- Chapter
- Export citation
Unstable trees
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 141-144
-
- Chapter
- Export citation
Cut-set lattices of graphs
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 35-36
-
- Chapter
- Export citation
On a family of planar bicritical graphs
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 103-108
-
- Chapter
- Export citation
Distance-transitive graphs
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 145-154
-
- Chapter
- Export citation
Analogues of Heawood's theorem
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 27-34
-
- Chapter
- Export citation
On the enumeration of partially ordered sets of integers
-
-
- Book:
- Combinatorics
- Published online:
- 05 April 2013
- Print publication:
- 21 November 1974, pp 109-124
-
- Chapter
- Export citation
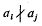 whenever
whenever 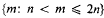
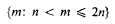
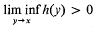 for all
for all 