Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Distinct values of Euler's ø-function
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1976
-
- Article
- Export citation
A characterization of pisot numbers
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-34
- Print publication:
- June 1976
-
- Article
- Export citation
Space tiling zonotopes
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 202-211
- Print publication:
- December 1975
-
- Article
- Export citation
Galois module structure of classgroups and units
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-160
- Print publication:
- December 1975
-
- Article
- Export citation
A model for the classifying space of an extra special p-group
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-187
- Print publication:
- December 1975
-
- Article
- Export citation
MTK volume 22 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1975
-
- Article
-
- You have access
- Export citation
Bombieri's theorem in short intervals
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-194
- Print publication:
- December 1975
-
- Article
- Export citation
Neighbourliness of centrally symmetric polytopes in high dimensions
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 176-181
- Print publication:
- December 1975
-
- Article
- Export citation
On norms of integers in a full module of an algebraic number field and the distribution of values of binary integral quadratic forms
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-111
- Print publication:
- December 1975
-
- Article
- Export citation
On the fractional parts of the sum of powers of rational numbers
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 154-155
- Print publication:
- December 1975
-
- Article
- Export citation
A property of polynomials over a finite field
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-153
- Print publication:
- December 1975
-
- Article
- Export citation
On the two-dimensional inviscid flow from symmetric slowly varying nozzles
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-140
- Print publication:
- December 1975
-
- Article
- Export citation
The existence of a centrally symmetric convex body with central sections that are unexpectedly small
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-175
- Print publication:
- December 1975
-
- Article
- Export citation
Absolutely non-measurable and singular co-analytic set
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-163
- Print publication:
- December 1975
-
- Article
- Export citation
Spira's theorems on complete linear proofs of systems of linear inequalities
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 112-121
- Print publication:
- December 1975
-
- Article
- Export citation
Discrete parabolic representations of link groups
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-150
- Print publication:
- December 1975
-
- Article
- Export citation
A set of infinite measure whose ratio set does not contain a given sequence
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 195-201
- Print publication:
- December 1975
-
- Article
- Export citation
Short surface waves due to a heaving torus
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-134
- Print publication:
- December 1975
-
- Article
- Export citation
Index to volume 22
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, p. 212
- Print publication:
- December 1975
-
- Article
- Export citation
On the periods of Abelian functions in two variables
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-107
- Print publication:
- December 1975
-
- Article
- Export citation
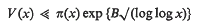
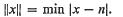
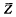 in
in 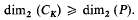
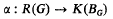
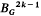 denotes the (2k − l)-skeleton of
denotes the (2k − l)-skeleton of 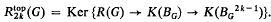
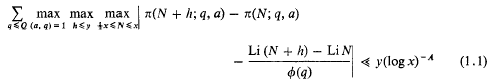
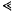 denotes as usual the suppression of an absolute constant,
denotes as usual the suppression of an absolute constant, 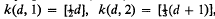 , and
, and 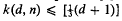 for
for 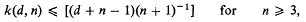
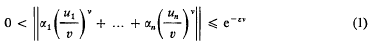
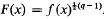 . Consider the continued fraction expansions
. Consider the continued fraction expansions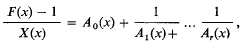
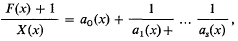
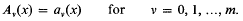
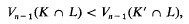
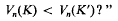
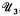 , and that each discrete subgroup of PSL(ℂ) acts discontinuously on
, and that each discrete subgroup of PSL(ℂ) acts discontinuously on 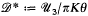 . The present paper is a study of the general relations between the algebraic properties of a discrete image
. The present paper is a study of the general relations between the algebraic properties of a discrete image 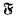 of Abelian functions on the quotient space C
of Abelian functions on the quotient space C