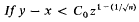Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Index
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 100-101
-
- Chapter
- Export citation
Appendix B - The Perron-Frobenius theorem
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 97-99
-
- Chapter
- Export citation
Chapter 5 - Prospects
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 81-94
-
- Chapter
- Export citation
Theorems of Novikov type
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-114
- Print publication:
- June 1977
-
- Article
- Export citation
Projective representations of the infinite orthogonal group
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-121
- Print publication:
- June 1977
-
- Article
- Export citation
A set in L containing regularizing families for ultrafilters
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-51
- Print publication:
- June 1977
-
- Article
- Export citation
On the resonant interaction between a surface wave and a weak surface current
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-49
- Print publication:
- June 1977
-
- Article
- Export citation
A note on the motion of a closely fitting plug along a fluid-filled tube
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-70
- Print publication:
- June 1977
-
- Article
- Export citation
Intersections of translates of convex sets
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-129
- Print publication:
- June 1977
-
- Article
- Export citation
Lebesgue measures on topological spaces
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 52-59
- Print publication:
- June 1977
-
- Article
- Export citation
A theorem on cubes
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-62
- Print publication:
- June 1977
-
- Article
- Export citation
Radon partitions and a new notion of independence in affine and projective spaces
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 86-96
- Print publication:
- June 1977
-
- Article
- Export citation
A note on involutary division algebras of the second kind
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-36
- Print publication:
- June 1977
-
- Article
- Export citation
Structure of l-class groups of certain number fields and ℤl-extensions
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 16-33
- Print publication:
- June 1977
-
- Article
- Export citation
MTK volume 24 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1977
-
- Article
-
- You have access
- Export citation
Nonclosed simplices and quasi-simplices
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-85
- Print publication:
- June 1977
-
- Article
- Export citation
The class number of pure fields of prime degree
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, p. 133
- Print publication:
- June 1977
-
- Article
- Export citation
Localization, completion and infinite complexes
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-15
- Print publication:
- June 1977
-
- Article
- Export citation
A note on the Fermat equation
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 130-132
- Print publication:
- June 1977
-
- Article
- Export citation
Index to volume 23
-
- Journal:
- Mathematika / Volume 23 / Issue 2 / December 1976
- Published online by Cambridge University Press:
- 26 February 2010, p. 228
- Print publication:
- December 1976
-
- Article
- Export citation
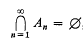
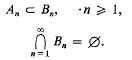
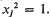
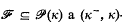 regularizing family (for short, a regularizing family) if Card ℱ = k and
regularizing family (for short, a regularizing family) if Card ℱ = k and 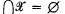 for each
for each 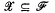 with Card
with Card 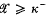 . In [7], Prikry proved, assuming
. In [7], Prikry proved, assuming 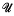 is an ultrafilter on
is an ultrafilter on 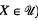 ) then
) then 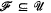 forms a regularizing family).†
forms a regularizing family).†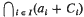 is non-empty for all families (
is non-empty for all families (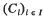 to have the intersection property.
to have the intersection property.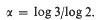
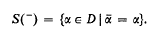
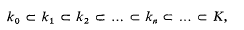
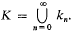 Let
Let 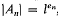 , with
, with
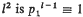 if
if