Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Extremal self-dual lattices exist only in dimensions 1 to 8, 12, 14, 15, 23, and 24
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-43
- Print publication:
- June 1978
-
- Article
- Export citation
Euler factors for p-adic L-functions
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-75
- Print publication:
- June 1978
-
- Article
- Export citation
Lebesgue density influences Hausdorff measure; large sets surface-like from many directions
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-119
- Print publication:
- June 1978
-
- Article
- Export citation
A support characterization of zonotopes
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-16
- Print publication:
- June 1978
-
- Article
- Export citation
Waves and conjugate streams with vorticity
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-150
- Print publication:
- June 1978
-
- Article
- Export citation
One-class genera of positive quadratic forms in nine and ten variables
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-67
- Print publication:
- June 1978
-
- Article
- Export citation
MTK volume 25 issue 1 Front Matter
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1978
-
- Article
-
- You have access
- Export citation
Fractional parts of several polynomials—II
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-93
- Print publication:
- June 1978
-
- Article
- Export citation
Kinematic measures for sets of colliding convex Bodies
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-12
- Print publication:
- June 1978
-
- Article
- Export citation
Lagrange's theorem for weak functions of several variables
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 160-178
- Print publication:
- June 1978
-
- Article
- Export citation
Laminar flow over a small unsteady hump on a flat plate
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-35
- Print publication:
- June 1978
-
- Article
- Export citation
An example concerning completion regular measures, images of measurable sets and measurable selections
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-124
- Print publication:
- June 1978
-
- Article
- Export citation
A triangulation criterion
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 110-114
- Print publication:
- June 1978
-
- Article
- Export citation
Some intersection and union theorems for several families of finite sets
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-128
- Print publication:
- June 1978
-
- Article
- Export citation
Small differences between consecutive primes II
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
- Print publication:
- December 1977
-
- Article
- Export citation
A class number relation in Frobenius extensions of number fields
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-225
- Print publication:
- December 1977
-
- Article
- Export citation
On the differences of additive arithmetic functions
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-165
- Print publication:
- December 1977
-
- Article
- Export citation
Euler's ø-function and its iterates
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-177
- Print publication:
- December 1977
-
- Article
- Export citation
Rank one elements of Banach algebras
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-181
- Print publication:
- December 1977
-
- Article
- Export citation
Generation of σ-algebras, Baire sets and descriptive Borel sets
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-256
- Print publication:
- December 1977
-
- Article
- Export citation
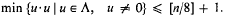
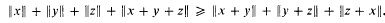
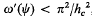 , where
, where 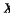 supporting a Radon probability measure μ and a continuous map ø :
supporting a Radon probability measure μ and a continuous map ø : 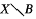 and
and 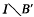 homeomorphic
homeomorphic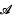 is a collection of distinct subsets of {1, …,
is a collection of distinct subsets of {1, …, 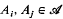 ,
, 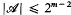 .
.

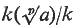 where
where