Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
The effective compliance of perforated screens
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-215
- Print publication:
- December 1977
-
- Article
- Export citation
Moments of last exit times
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 266-269
- Print publication:
- December 1977
-
- Article
- Export citation
On the distribution of αp modulo 1
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-141
- Print publication:
- December 1977
-
- Article
- Export citation
K-analytic spaces with metrizable compacta
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 257-261
- Print publication:
- December 1977
-
- Article
- Export citation
MTK volume 24 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1977
-
- Article
-
- You have access
- Export citation
Continuants with bounded digits
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 166-172
- Print publication:
- December 1977
-
- Article
- Export citation
Contact forms on 1-connected 5-manifolds
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 237-240
- Print publication:
- December 1977
-
- Article
- Export citation
Index to volume 24
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, p. 270
- Print publication:
- December 1977
-
- Article
- Export citation
The mean value of the derivative of the Dedekind zeta-function of a real quadratic field
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 226-236
- Print publication:
- December 1977
-
- Article
- Export citation
A C∞ curve of spectral non-synthesis
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-192
- Print publication:
- December 1977
-
- Article
- Export citation
An asymptotic expansion for the Wedderburn–Etherington sequence
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 262-265
- Print publication:
- December 1977
-
- Article
- Export citation
A lower bound for the L1-norm of certain exponential sums
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-188
- Print publication:
- December 1977
-
- Article
- Export citation
Centrally symmetric convex sets and mixed volumes
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-198
- Print publication:
- December 1977
-
- Article
- Export citation
Chapter 4 - Expansions
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 60-80
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp i-iv
-
- Chapter
- Export citation
Chapter 3 - Duality
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 39-59
-
- Chapter
- Export citation
Appendix A - Distributive identities
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 95-96
-
- Chapter
- Export citation
Chapter 1 - Preview
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 1-17
-
- Chapter
- Export citation
Contents
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp v-vi
-
- Chapter
- Export citation
Chapter 2 - Methods
-
- Book:
- Interaction Models
- Published online:
- 16 March 2010
- Print publication:
- 24 November 1977, pp 18-38
-
- Chapter
- Export citation
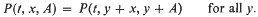
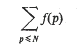
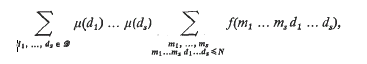
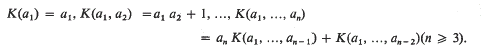
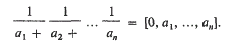
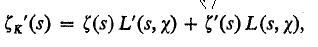
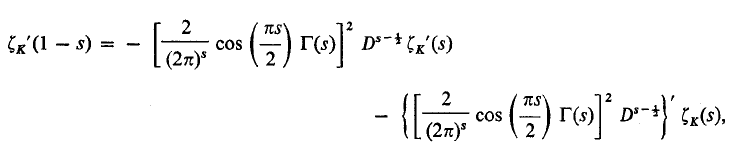
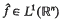 is defind by
is defind by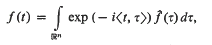
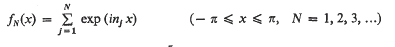
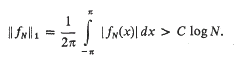
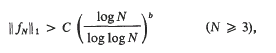
 denote the class of all compact convex sets in Euclidean
denote the class of all compact convex sets in Euclidean 