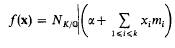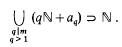Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
7 - Geometries in finite projective and affine spaces
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 17 March 2010
- Print publication:
- 09 August 1979, pp 181-210
-
- Chapter
- Export citation
Determination of a binary quadratic form by its values at integer points
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-75
- Print publication:
- June 1979
-
- Article
- Export citation
On a problem of Barban and Vehov
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-71
- Print publication:
- June 1979
-
- Article
- Export citation
A distal property of groups and the growth of connected locally compact groups
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-98
- Print publication:
- June 1979
-
- Article
- Export citation
Packing smooth curves in Rq
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-12
- Print publication:
- June 1979
-
- Article
- Export citation
Universal fixed messages and the Rivest-Shamir-Adleman cryptosystem
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 44-52
- Print publication:
- June 1979
-
- Article
- Export citation
MTK volume 26 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1979
-
- Article
-
- You have access
- Export citation
On CS-closed sets
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-32
- Print publication:
- June 1979
-
- Article
- Export citation
Borel isomorphisms at the first level—I
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-156
- Print publication:
- June 1979
-
- Article
- Export citation
Inner contact measures
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
- Print publication:
- June 1979
-
- Article
- Export citation
Lusin's theorem for measure preserving homeomorphisms
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-43
- Print publication:
- June 1979
-
- Article
- Export citation
Stable, fragile and absolutely symmetric quadratic forms
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-79
- Print publication:
- June 1979
-
- Article
- Export citation
The ambiguous class group and the genius group of certain non-normal extensions
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-124
- Print publication:
- June 1979
-
- Article
- Export citation
Category algebras of complete metric spaces
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-17
- Print publication:
- June 1979
-
- Article
- Export citation
An approach to the zero-divisor question for group rings
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-93
- Print publication:
- June 1979
-
- Article
- Export citation
The distribution of integral and prime-integral values of systems of full-norm polynomials and affine-decomposable polynomials
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-87
- Print publication:
- June 1979
-
- Article
- Export citation
Ellipsoids defined by Banach ideal norms
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-29
- Print publication:
- June 1979
-
- Article
- Export citation
An embedding for groups with length functions
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-102
- Print publication:
- June 1979
-
- Article
- Export citation
Covering systems of congruences, a negative result
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-61
- Print publication:
- June 1979
-
- Article
- Export citation
Outer automorphisms and non-trivial Picard groups
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-105
- Print publication:
- June 1979
-
- Article
- Export citation
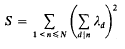
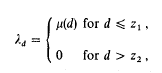
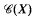 of
of 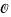 denote the ring of integers of
denote the ring of integers of