Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Convex bodies which tile space by translation
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-121
- Print publication:
- June 1980
-
- Article
- Export citation
Sections of Sets of zero Lebesgue measure
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-96
- Print publication:
- June 1980
-
- Article
- Export citation
Proof of D. J. Newman's coprime mapping conjecture
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-83
- Print publication:
- June 1980
-
- Article
- Export citation
The measure of the s-skeleton of a convex body
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-301
- Print publication:
- December 1979
-
- Article
- Export citation
Nearly parallel vectors
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-268
- Print publication:
- December 1979
-
- Article
- Export citation
On a problem of Barban and Vehov, Corrigendum
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, p. 306
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Denumerable compact metric spaces admit isometry-invariant finitely additive measures
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 184-186
- Print publication:
- December 1979
-
- Article
- Export citation
Instability of flow through pipes of general cross-section, Part 1
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-210
- Print publication:
- December 1979
-
- Article
- Export citation
On the Mertens conjecture for cusp forms
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 236-249
- Print publication:
- December 1979
-
- Article
- Export citation
Mass transport induced by standing interfacial waves
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 224-235
- Print publication:
- December 1979
-
- Article
- Export citation
A decomposition theorem in tensor products of Archimedean vector lattices
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 302-305
- Print publication:
- December 1979
-
- Article
- Export citation
Index to volume 26
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, p. 307
- Print publication:
- December 1979
-
- Article
- Export citation
Borel isomorphisms at the first level, II
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-179
- Print publication:
- December 1979
-
- Article
- Export citation
Packing planes in ℝ3
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 180-183
- Print publication:
- December 1979
-
- Article
- Export citation
Symmetrization and currents
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 269-289
- Print publication:
- December 1979
-
- Article
- Export citation
Instability of flow through pipes of general cross-section, Part 2
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 211-223
- Print publication:
- December 1979
-
- Article
- Export citation
MTK volume 26 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Buchstab's sifting weights
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 250-257
- Print publication:
- December 1979
-
- Article
- Export citation
Note on the Projects
-
- Book:
- Permutation Groups and Combinatorial Structures
- Published online:
- 04 February 2010
- Print publication:
- 16 August 1979, pp viii-viii
-
- Chapter
- Export citation
Chapter 1 - Permutation Groups
-
- Book:
- Permutation Groups and Combinatorial Structures
- Published online:
- 04 February 2010
- Print publication:
- 16 August 1979, pp 1-23
-
- Chapter
- Export citation
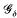 -set [see 6] and it is therefore measurable with respect to the
-set [see 6] and it is therefore measurable with respect to the 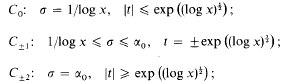
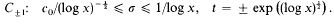
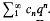 We shall assume that
We shall assume that 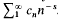 The series and the product
The series and the product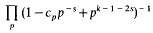
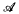 be a finite sequence of positive integers. If we want to show that
be a finite sequence of positive integers. If we want to show that 