Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Borel isomorphisms at the first level: Corrigenda et addenda
-
- Journal:
- Mathematika / Volume 27 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 236-260
- Print publication:
- December 1980
-
- Article
- Export citation
Continued fractions and Fourier transforms
-
- Journal:
- Mathematika / Volume 27 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 262-267
- Print publication:
- December 1980
-
- Article
- Export citation
Some remarks on fibrations of monoids and their classifying spaces
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-212
- Print publication:
- December 1980
-
- Article
- Export citation
On the number of square-full integers between successive squares
-
- Journal:
- Mathematika / Volume 27 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-178
- Print publication:
- December 1980
-
- Article
- Export citation
Determination of a binary quadratic form by its values at integer points: Acknowledgement
-
- Journal:
- Mathematika / Volume 27 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 26 February 2010, p. 188
- Print publication:
- December 1980
-
- Article
- Export citation
12 - Finite geometries and codes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 76-83
-
- Chapter
- Export citation
9 - Codes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 61-67
-
- Chapter
- Export citation
13 - Self-orthogonal codes, designs and projective planes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 84-94
-
- Chapter
- Export citation
14 - Quadratic residue codes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 95-106
-
- Chapter
- Export citation
17 - Association schemes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 124-135
-
- Chapter
- Export citation
1 - A brief introduction to design theory
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 1-15
-
- Chapter
- Export citation
Preface
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp vii-viii
-
- Chapter
- Export citation
5 - Strongly regular graphs with no triangles
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 37-44
-
- Chapter
- Export citation
6 - Polarities of designs
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 45-48
-
- Chapter
- Export citation
8 - 1-factorisations of K6
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 56-60
-
- Chapter
- Export citation
3 - Quasi-symmetric designs
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 25-31
-
- Chapter
- Export citation
10 - Cyclic codes
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 68-73
-
- Chapter
- Export citation
7 - Extensions of graphs
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 49-55
-
- Chapter
- Export citation
Index
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 145-147
-
- Chapter
- Export citation
11 - Threshold decoding
-
- Book:
- Graphs, Codes and Designs
- Published online:
- 16 March 2010
- Print publication:
- 31 July 1980, pp 74-75
-
- Chapter
- Export citation
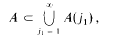
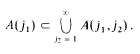
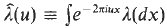 vanishes at infinity. Aside from the Riemann-Lebesgue Lemma, no purely metrical property of
vanishes at infinity. Aside from the Riemann-Lebesgue Lemma, no purely metrical property of 