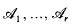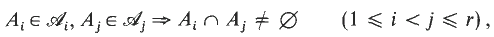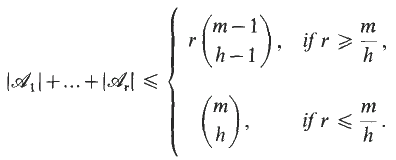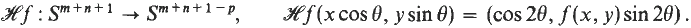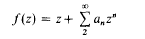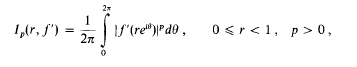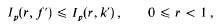Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
The geometry of planar graphs
-
-
- Book:
- Combinatorics
- Published online:
- 16 March 2010
- Print publication:
- 03 September 1981, pp 124-150
-
- Chapter
- Export citation
Ovals in a projective plane of order 10
-
-
- Book:
- Combinatorics
- Published online:
- 16 March 2010
- Print publication:
- 03 September 1981, pp 187-190
-
- Chapter
- Export citation
On ext(G2)
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-85
- Print publication:
- June 1981
-
- Article
- Export citation
The transformation of concentric circles into concentric rectangles
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-152
- Print publication:
- June 1981
-
- Article
- Export citation
On ordered set systems and some conjectures related to the erdös–ko–rado theorem and turán's theorem
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-66
- Print publication:
- June 1981
-
- Article
- Export citation
An acknowledgement of priority
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, p. 87
- Print publication:
- June 1981
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, p. 86
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Energy decay in a problem of linear thermoelasticity
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-115
- Print publication:
- June 1981
-
- Article
- Export citation
The necessity of sigma-finiteness in the radon–nikodym theorem
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- June 1981
-
- Article
- Export citation
MTK volume 28 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Consequences of the kahn–priddy theorem in homotopy and geometry
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-78
- Print publication:
- June 1981
-
- Article
- Export citation
An integral mean inequality for starlike functions
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-98
- Print publication:
- June 1981
-
- Article
- Export citation
Patterns on the 2-Sphere
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-35
- Print publication:
- June 1981
-
- Article
- Export citation
Encoding orders and trees in binary relations
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-71
- Print publication:
- June 1981
-
- Article
- Export citation
Real classification of complex conics
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-53
- Print publication:
- June 1981
-
- Article
- Export citation
Uniform asymptotic solutions of the orr–sommerfeld equation
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-140
- Print publication:
- June 1981
-
- Article
- Export citation
Regular cliques in graphs and special 1½ designs
-
-
- Book:
- Finite Geometries and Designs
- Published online:
- 05 April 2013
- Print publication:
- 16 April 1981, pp 244-259
-
- Chapter
- Export citation
On k-sets of class [0,1,2,n]2 in PG(r,q)
-
-
- Book:
- Finite Geometries and Designs
- Published online:
- 05 April 2013
- Print publication:
- 16 April 1981, pp 31-39
-
- Chapter
- Export citation
Some translation planes of order 81
-
-
- Book:
- Finite Geometries and Designs
- Published online:
- 05 April 2013
- Print publication:
- 16 April 1981, pp 114-118
-
- Chapter
- Export citation
On k-sets of type (m,n) in a Steiner system S(2, l, v)
-
-
- Book:
- Finite Geometries and Designs
- Published online:
- 05 April 2013
- Print publication:
- 16 April 1981, pp 104-113
-
- Chapter
- Export citation