Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
CHAPTER 4 - DIFFERENCE SETS
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 120-187
-
- Chapter
- Export citation
Contents
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp vii-viii
-
- Chapter
- Export citation
REFERENCES
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 294-303
-
- Chapter
- Export citation
The square mean of Dirichlet series associated with cusp forms
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-295
- Print publication:
- December 1982
-
- Article
- Export citation
Further lattice packings in high dimensions
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-180
- Print publication:
- December 1982
-
- Article
- Export citation
Irrationality of lattices in finite characteristic
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-230
- Print publication:
- December 1982
-
- Article
- Export citation
Further solutions of the Falkner–Skan equation for β = – 1 and γ = 0
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-248
- Print publication:
- December 1982
-
- Article
- Export citation
Packing and covering with convex discs
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 181-193
- Print publication:
- December 1982
-
- Article
- Export citation
Connectivity and freely rolling convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 249-259
- Print publication:
- December 1982
-
- Article
- Export citation
MTK volume 29 issue 2 Back matter
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
On the Riemann zeta-function ζ(s)—Gaps between sign changes of S(t)
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-269
- Print publication:
- December 1982
-
- Article
- Export citation
Power mean values of the Riemann zeta-function
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 202-212
- Print publication:
- December 1982
-
- Article
- Export citation
MTK volume 29 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
The recognition of certain Hausdorff like measures
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 260-263
- Print publication:
- December 1982
-
- Article
- Export citation
Slices of L. Fejes Tóth's sausage conjecture
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 194-201
- Print publication:
- December 1982
-
- Article
- Export citation
On the Mertens conjecture for cusp forms
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-226
- Print publication:
- December 1982
-
- Article
- Export citation
Exponential sums connected with Ramanujan's function τ(n)
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-277
- Print publication:
- December 1982
-
- Article
- Export citation
Local cohomology and modules of generalized fractions
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 296-306
- Print publication:
- December 1982
-
- Article
- Export citation
MTK volume 29 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Totally ordered measure spaces and their Lp algebras
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-54
- Print publication:
- June 1982
-
- Article
- Export citation
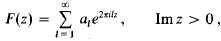
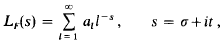
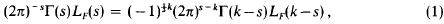
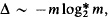 , as
, as 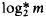 is the smallest value of
is the smallest value of 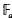 be the finite field with
be the finite field with 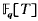 is considered as an analogue of the ring of rational integers ℤ. Completing the quotient field
is considered as an analogue of the ring of rational integers ℤ. Completing the quotient field 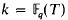 with respect to the normalized valuation at ∞, and then taking algebraic closure, we obtained the field
with respect to the normalized valuation at ∞, and then taking algebraic closure, we obtained the field 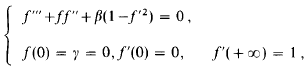
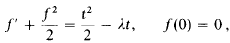
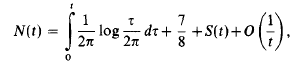
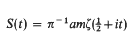
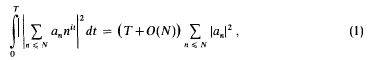
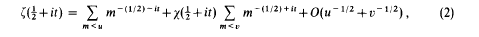
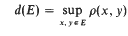
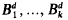 be
be 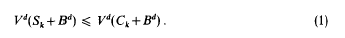
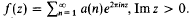 We assume further that
We assume further that 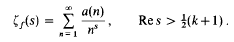
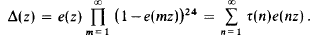
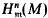 may be viewed as a module of generalized fractions of
may be viewed as a module of generalized fractions of 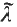 on Ĩ such that τ(
on Ĩ such that τ(