Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
On Kruskal's cascades and counting containments in a set of subsets
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-141
- Print publication:
- June 1983
-
- Article
- Export citation
Transcendental numbers arising from Drinfeld modules
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-66
- Print publication:
- June 1983
-
- Article
- Export citation
MTK volume 30 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
On the general solution of a linear second order equation with variable coefficients
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-103
- Print publication:
- June 1983
-
- Article
- Export citation
On the densest packing of convex discs
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1983
-
- Article
- Export citation
CHAPTER 1 - SYMMETRIC DESIGNS
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 1-41
-
- Chapter
- Export citation
C - Invariant Factors
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 262-264
-
- Chapter
- Export citation
APPENDICES
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp -
-
- Chapter
- Export citation
CHAPTER 6 - OPEN QUESTIONS
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 223-244
-
- Chapter
- Export citation
D - Representation Theory
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 265-283
-
- Chapter
- Export citation
CHAPTER 3 - AUTOMORPHISMS
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 78-119
-
- Chapter
- Export citation
A - Permutation Groups
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 245-249
-
- Chapter
- Export citation
E - Cyclotomic Fields
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 284-285
-
- Chapter
- Export citation
CHAPTER 2 - AN ALGEBRAIC APPROACH
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 42-77
-
- Chapter
- Export citation
Preface
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp ix-xii
-
- Chapter
- Export citation
F - P-adic Numbers
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 286-293
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp i-vi
-
- Chapter
- Export citation
B - Bilinear and Quadratic Forms
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 250-261
-
- Chapter
- Export citation
CHAPTER 5 - MULTIPLIER THEOREMS
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 188-222
-
- Chapter
- Export citation
INDEX
-
- Book:
- Symmetric Designs
- Published online:
- 16 March 2010
- Print publication:
- 20 January 1983, pp 304-306
-
- Chapter
- Export citation
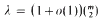 ,
, 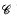 be a smooth projective, geometrically irreducible curve over a finite field
be a smooth projective, geometrically irreducible curve over a finite field 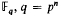 . We fix a rational point ∞on
. We fix a rational point ∞on 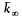 whose elements will be called “numbers”.
whose elements will be called “numbers”.