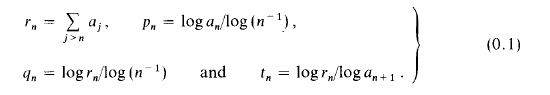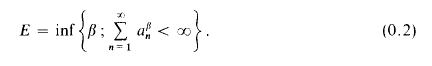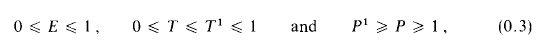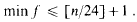Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
On the oscillation of solutions of linear differential equations
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 214-226
- Print publication:
- December 1984
-
- Article
- Export citation
Theories for the diffraction of three-dimensional surface waves by plane vertical obstacles
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-195
- Print publication:
- December 1984
-
- Article
- Export citation
Integers free of large prime factors and the Riemann hypothesis
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-271
- Print publication:
- December 1984
-
- Article
- Export citation
On the additivity and cofinality of Radon measures
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-335
- Print publication:
- December 1984
-
- Article
- Export citation
Universal graphs without large bipartite subgraphs
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 282-290
- Print publication:
- December 1984
-
- Article
- Export citation
Gale transforms and closed faces of infinite dimensional polytopes
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 291-304
- Print publication:
- December 1984
-
- Article
- Export citation
Short-length instabilities, breakdown and initial value problems in dynamic stall
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 163-177
- Print publication:
- December 1984
-
- Article
- Export citation
On the representation of integers with large square factors by positive definite ternary quadratic forms
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 252-257
- Print publication:
- December 1984
-
- Article
- Export citation
Centrally symmetric convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-322
- Print publication:
- December 1984
-
- Article
- Export citation
Fourier transforms and descriptive set theory
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 336-339
- Print publication:
- December 1984
-
- Article
- Export citation
Weierstrass equations and the minimal discriminant of an elliptic curve
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-251
- Print publication:
- December 1984
-
- Article
- Export citation
MTK volume 31 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
Continuous dependence and uniqueness theorems in boundary-initial value problems for a class of porous bodies occupying bounded or unbounded domains
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 196-213
- Print publication:
- December 1984
-
- Article
- Export citation
Index to volume 31
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 340-341
- Print publication:
- December 1984
-
- Article
- Export citation
On a construction of the universal field of fractions of a free algebra
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-233
- Print publication:
- December 1984
-
- Article
- Export citation
An Fσ semigroup of zero measure which contains a translate of every countable set
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 272-281
- Print publication:
- December 1984
-
- Article
- Export citation
The average orders of Hooley's Δr-functions
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-109
- Print publication:
- June 1984
-
- Article
- Export citation
The divisor function at consecutive integers
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-149
- Print publication:
- June 1984
-
- Article
- Export citation
Some relations connecting measures of convergence for series with non-increasing terms
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
- Print publication:
- June 1984
-
- Article
- Export citation
An application of Siegel's formula over quaternion orders
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-16
- Print publication:
- June 1984
-
- Article
- Export citation
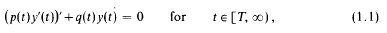
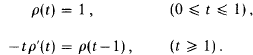
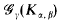 denote the class of all graphs on γ vertices having no subgraph isomorphic to
denote the class of all graphs on γ vertices having no subgraph isomorphic to 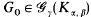 is called universal if every
is called universal if every 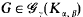 can be embedded into
can be embedded into 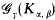 has a universal element, if, and only if, (i) γ >
has a universal element, if, and only if, (i) γ > 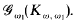 .
.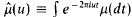 its Fourier-Stieltjes transform. We define ℛ to be the set of μ with
its Fourier-Stieltjes transform. We define ℛ to be the set of μ with 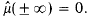 When μ ∈ ℛ and φ is of class
When μ ∈ ℛ and φ is of class 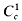 (continuously differentiable of compact support), the identity
(continuously differentiable of compact support), the identity 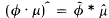 shows that θ · μ ∈ ℛ.
shows that θ · μ ∈ ℛ.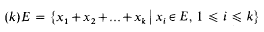
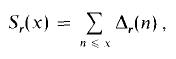
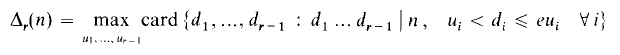
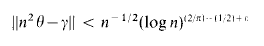
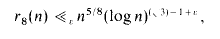
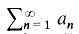 converges; then clearly
converges; then clearly